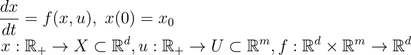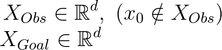Collision-free Navigation
|
Collision-free navigation is a fundamental required capability of robots such that they can operate and function as autonomous reliable systems. With the perception systems becoming everyday more capable and especially since real-time 3D perception of the environment became possible, motion planning for obstacle-free flight became a critical loop of aerial robotics. Eventually, aerial robotics are desired to be able to express the navigational agility in cluttered environments observed in nature. Figure 1 presents a hawk flying through two trees. It corresponds to a long-standing paradigm of what an aerial robot should -conceptually- be able to do in the near future.
Collision-free navigation is a field on its own. Here we will briefly overview the basic problem formulation and examine one of its possible solutions. In particular, we will present the Rapidly-exploring Random Tree method. |
Figure 1: A hawk flying through two trees in a forest. Image from a video by Smithsonian Channel - https://youtu.be/HYGz32iv1vw
|
Kinodynamic Motion Planning Problem
Given a dynamic system described by the Ordinary Differential Equation (ODE):
Given a dynamic system described by the Ordinary Differential Equation (ODE):
where x is the state trajectory, u a bounded measurable control signal and f is a Lipschitz function. Now further let:
corresponding to the set of obstacles (characterizing the obstacle region) and the goal set (characterizing the goal region). The goal of the kinodynamic motion planning problem is to find a control signal u such that the solution of the ODE describing the vehicle dynamics satisfies that all state trajectories x do not intersect the obstacle set XObs and there exists a time instant such that x goes through the desired goal set XGoal. If no such solution exists, then the motion planning solution should return failure.
It is highlighted that even a simple version of this problem is PSPACE-hard.
It is highlighted that even a simple version of this problem is PSPACE-hard.
|
Rapidly-exploring Random Tree algorithm
One particularly successful approach to the problem of finding admissible collision-free paths (even though not optimal) is based on the concept of incremental sampling-based algorithms for motion planning. Specifically, the method of Rapidly-exploring Random Tree (RRT) relies on the idea of exploring a tree of feasible trajectories of the system via random sampling. Below, the main steps of this algorithm are presented. RRT Algorithm:
|
Video: Visualization of the RRT steps to find an admissible solution.
|
|
Extend Procedure:
|
|
Completeness guarantees
Optimal Collision-free Navigation
Although RRT is not optimal, one variation of it, RRT* is proven to be asymptotically optimal. Details on that algorithm can be found in the following contribution:
Karaman Sertac, and Emilio Frazzoli, "Sampling-based algorithms for optimal motion planning", The International Journal of Robotics Research 30.7 (2011): 846-894.
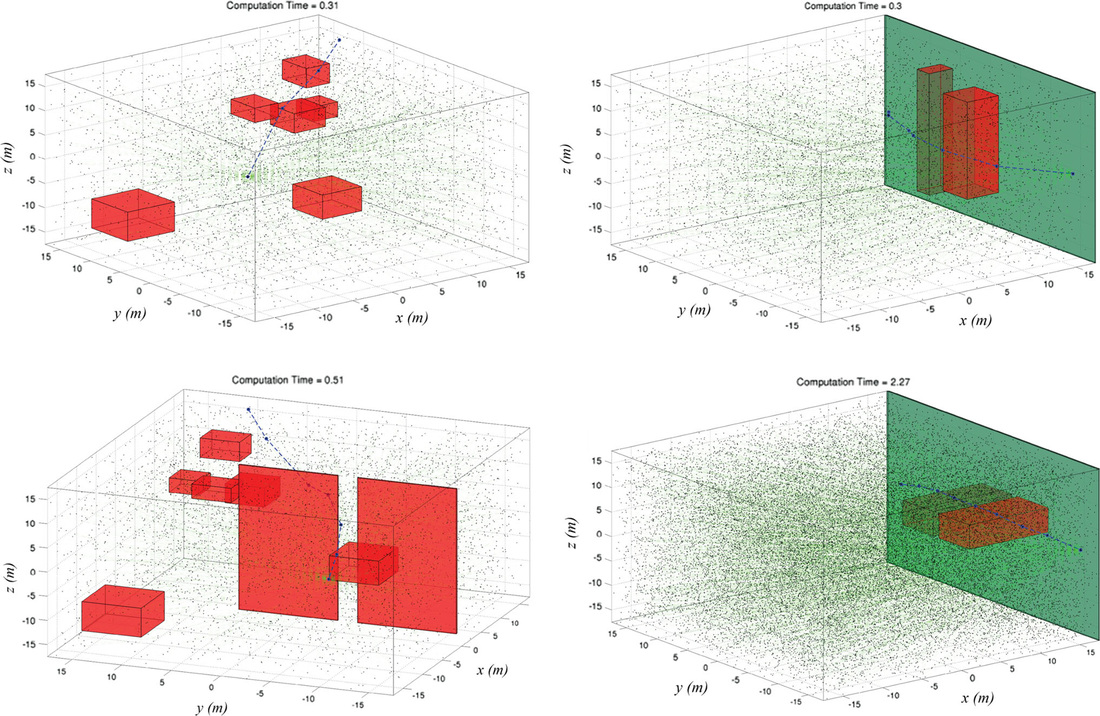
While indicative solutions are presented in Figure 2.
- Probabilistic completeness: The probability of finding a solution, if one exists, approaches to one (1) as the number of samples approaches infinity
Optimal Collision-free Navigation
Although RRT is not optimal, one variation of it, RRT* is proven to be asymptotically optimal. Details on that algorithm can be found in the following contribution:
Karaman Sertac, and Emilio Frazzoli, "Sampling-based algorithms for optimal motion planning", The International Journal of Robotics Research 30.7 (2011): 846-894.
While indicative solutions are presented in Figure 2.
Figure 2: Indicative RRT* solutions. The results are taken from the following paper: K. Alexis, G. Darivianakis, M. Burri, and R. Siegwart, "Aerial robotic contact-based inspection: planning and control", Autonomous Robots, Springer US, DOI: 10.1007/s10514-015-9485-5, ISSN: 0929-5593, http://dx.doi.org/10.1007/s10514-015-9485-5