Structural Inspection Path Planning

Structural Inspection Path Planning considers the problem of finding a feasible - possibly optimal or close-to-optimal - path for an aerial robot such that its onboard perception system (e.g. camera, LiDAR) "covers" the whole surface of a desired structure. Essentially, it is a problem of complete coverage. As it corresponds to an active research topic, a variety of methods have been proposed and the scientific community is still investigating path planning strategies that are able to provide good inspection solutions in close-to-real-time computation effort. Within the framework of this document, we will overview the approach proposed in the following two contributions:

• A. Bircher, K. Alexis, M. Burri, P. Oettershagen, S. Omari, T. Mantel, R. Siegwart, "Structural Inspection Path Planning via Iterative Viewpoint Resampling with Application to Aerial Robotics", IEEE International Conference on Robotics & Automation, May 26-30, 2015 (ICRA 2015), Seattle, Washington, USA .
• A. Bircher, M. Kamel, K. Alexis, M. Burri, P. Oettershagen, S. Omari, T. Mantel, R. Siegwart, "Three-dimensional Coverage Path Planning via Viewpoint Resampling and Tour Optimization for Aerial Robots", Autonomous Robots, Springer US, DOI: 10.1007/s10514-015-9517-1, ISSN: 1573-7527
• Open-Source Git Repo: https://github.com/ethz-asl/StructuralInspectionPlanner 
• Experimental Datasets: https://github.com/ethz-asl/StructuralInspectionPlanner/wiki/Example-Results

​The goal of a Structural Inspection Path Planning design is to be able to provide full coverage solutions that are of low cost (in terms of overall path distance or time-of-travel), are computed in short time and with low computational load, while accounting for motion constraints of the vehicle and sensor limitations (e.g. Field of View). 

Among the most well-established approaches in the field, those that separate the overall problem into that of finding a minimal set of full-coverage viewpoints (Art Gallery Problem - AGP) and subsequently compute the optimal route among them (Traveling Salesman Problem - TSP) have been particularly successful. These methods often manage to produce good solutions in short time. However, they have two main limitations and problems, namely:

• They are prone to be suboptimal due to the two-step separation of the problem. 
• In specific cases they can lead to unfeasible solutions/paths (e.g. in the case of nonholonomic vehicles)

As a response to the abovementioned limitations, the problem Structural Inspection Planner (SIP), revisits the concept of 2-step optimization based inspection path planning. Essentially, SIP is driven by the idea that with a continuously (or very fast) sampling sensor, the number of viewpoints is not necessarily important but mostly their configuration in space. SIP does not search for a minimal set of viewpoints but rather for a set of full coverage viewpoints positioned such that the overall path gets minimized. SIP employs an iterative, viewpoint alternation and route re-computation 2-step optimization paradigm. Therefore, it guarantees to find feasible path solutions for both holonomic and nonholonomic vehicles and typically arrives at full-coverage solutions that are of low-cost. 

SIP Algorithm Pseudo-code

1. ​​Load the mesh model
   
2. k = 0
   
3. Sample Initial Viewpoint Configurations (Viewpoint Sampler)
   
4. Find a Collision-free path for all possible viewpoint combinations (BVS, RRT*)
   
5. Populate the Cost Matrix and Solve the Traveling Salesman Problem (LKH)
   
6. while running
   
   1. Re-sample Viewpoint Configurations (Viewpoint Sampler)
      
   2. Re-compute the Collision-free paths (BVS, RRT*)
      
   3. Re-populate the Cost Matrix and solve the new Traveling Salesman Problem to update the current best inspection tour (LKH)
      
   4. k = k + 1
      
7. end while
   
8. Return BestTour, CostBestTour

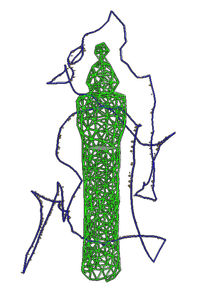
Figure 1: Indicative SIP solution

Viewpoint Optimization Process
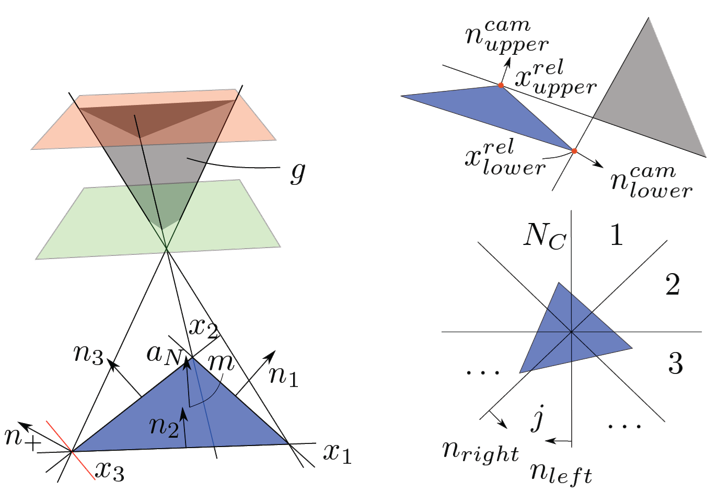
To perform the viewpoint optimization process, SIP relies on a mechanism based on a convex optimization methods. More specifically, admissible viewpoints are optimized for distance to the neighboring viewpoints. To guarantee that all viewpoints are admissible, the position solution g = [x,y,z] is constrained to allow finding an orientation for which the triangular face is visible:

To account for the limited camera Field of View (FoV), it imposes a revoluted 2D-cone constraint. This is a nonconvex problem which is then convexified by dividing the problem into Nc equal convex pieces. 

The concept is visualized in Figure 2. 

Figure 2: Viewpoint optimization process for finding admissible viewpoints that satisfy the sensing limitations of the robot. On the left the incidence angle constraints on a triangular surface are shown. On the right the camera constraints and the revoluted 2D-cone convexification is shown.  

Finally, the optimization problem to be solved at every SIP iteration takes the form: 
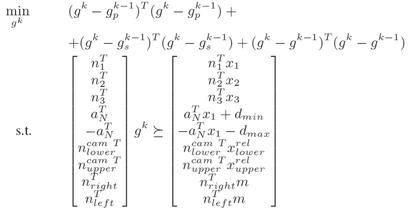
Minimize the sum of squared distances to the preceding viewpoint gp^{k-1}, the subsequent viewpoint gs^{k-1} and the current viewpoint in the old tour g^{k-1}. More formally: 

Which essentially consists of a Quadratic Program with Linear Constraints. The heading is determined according to:

SIP Point-to-Point Paths
In its current implementation, SIP relies on State-space sampling methods, while an extension to control-space sampling methods is possible. To find path solutions from one viewpoint to the other, it employs a Boundary Value Solver (BVS) for holonomic or nonholonomic vehicle configurations and relies on the optimal Rapidly-exploring Random Tree (RRT*) algorithm to derive collision-free paths.

SIP Tour Optimization
To solve for the per-iteration SIP tour optimization and derive the corresponding TSP solution, the method relies on the LKH solver. LKH is an effective implementation of the Lin-Kernighan heuristic for solving the Traveling Salesman Problem. The Lin-Kernighan solver (also called the Lin-Kernighan-Helsgaun solver) is among the most efficient solvers of the TSP and it is employing the concept of k-opt moves. ​The concept of k-moves is visualized in Figure 3. 

Figure 3: Visualization of the k-moves process. 

It is highlighted again, that the aforementioned two steps (viewpoint optimization and tour computation) are executed in an iterative fashion such that the algorithm derives solutions of improved cost. 

Simulation Studies
The following video presents an execution of the SIP algorithm and enables intuitive understanding of its operation. The first part of the video simply presents the mesh visualization process. 

Experimental Studies
The algorithm is actively used within the framework of inspection operations using both rotorcraft-type as well as fixed-wing aerial robots. More specifically, the Firefly MAV platform and the AtlantikSolar UAV were used - both equipped with the VI-Sensor. The platforms are shown in Figure 4. ​The following experimental datasets are available:

Using Fixed-Wing UAV:

• AtlantikSolar Inspection of the Marche-en-Famenne area using a Sony HDR-AS100VW 
• AtlantikSolar Inspection of the Marche-en-Famenne area using the VI-Sensor system
• AtlantikSolar Inspection of the Rothenthrum Moor area using a Sony HDR-AS100VW 
• AtlantikSolar Inspection of the Rothenthrum Moor area using the VI-Sensor system

Figure 4: Robot platforms used for the SIP experimental studies. Both fixed-wing and rotorcraft unmanned aerial vehicles were employed for evaluation purposes. 

Using Rotorcraft UAV:

• Firefly Hexarotor UAV Inspection of a Trolley at the ETH Zurich LEE building
• Firefly Hexarotor UAV Inspection of the ETH Polyterrasse

The two videos below present indicative subsets of the experimental datasets:

Learn more:
To learn more about the SIP algorithm essentials, you may go through the papers and study the code at our open-source repository: https://github.com/ethz-asl/StructuralInspectionPlanner/

As this corresponds to an open research topic, interested students may contact Dr. Kostas Alexis to discuss potential projects. 

Installation Instructions

As mentioned, the presented Structural Inspection Planner is released as an opens-source ROS package. Follow the instructions below to get it running on your ROS-enabled machine. 

StructuralInspectionPlanner

Beta version

The structural inspection path planning algorithm presented in our paper contribution [1] is released as an open-source toolbox. The algorithm assumes a triangular mesh representation of the structure and employs an alternating two-step optimization paradigm to find good viewpoints that together provide full coverage and a connecting path that has low cost. In every iteration, the viewpoints are chosen such that the connection cost is reduced and, subsequently, the tour is optimized. Vehicle and sensor limitations are respected within both steps. Sample implementations are provided for rotorcraft and fixed-wing unmanned aerial robots.

Additional functionality allows exportation of the computed paths to drone mission files. Supported systems are PX4/Pixhawk and DJI drones, as well as the RotorS simulator and will be extended in the future. (Refer to the utils section)

Installing the toolbox

To use the toolbox a ROS indigo installation with catkin set-up and the following extra packages are required:

libeigen3-dev
ros-indigo-tf
ros-indigo-rviz
ros-indigo-octomap
ros-indigo-octomap-msgs

Once these are there, a baseline example on how to get and install the tool is the following:

$ mkdir catkin_ws_repos # assuming you want to enter a new catkin directory
$ cd catkin_ws_repos # alternatively just cd your normal catkin workspace
$ mkdir src # assuming this folder does not exist
$ cd src/
$ catkin_init_workspace
$ git clone git@github.com:ethz-asl/StructuralInspectionPlanner.git
$ cd ..
$ catkin_make
$ source devel/setup.bash

The build process should then be executed and successfully complete. Subsequently open two separate shells and run the following two commands to execute the baseline demo of the algorithm:

Shell #1

roslaunch koptplanner kopt.launch

Shell #2

rosrun request request 

For visualization puprposes, a 3rd terminal has to be launched:

Shell #3

rosrun rviz rviz

Add the necessary displays:

‘Path’ on topic ‘visualization_marker’
‘Marker’ on topic ‘viewpoint_marker’
‘Path’ on topic ‘stl_mesh’
‘Marker’ on topic ‘scenario’

To display the progress, chose ‘/kopt_frame’ as fixed frame or publish a suitable transform.

Detailed Documentation

Detailed documentation may be found at the Wiki!

References:

1. A. Bircher, K. Alexis, M. Burri, P. Oettershagen, S. Omari, T. Mantel and R. Siegwart, “Structural inspection path planning via iterative viewpoint resampling with application to aerial robotics,” in Robotics and Automation (ICRA), 2015 IEEE International Conference on, May 2015, pp. 6423–6430.
2. K. Helsguan, “An effective implementation of the lin-kernighan traveling salesman heuristic”, European Journal of Operational Research, vol. 126, no. 1, pp. 106-130, 2000.
3. H.J. Ferreau and A. Potschka and C. Kirches, “qpOASES”
4. S. Karaman and E. Frazzoli, “Sampling-based algorithms for optimal motion planning”, International Journal of Robotics Research”, vol. 30, no. 7, pp. 846-894, 2011

If you use this software in a scientific publication, please cite the following paper:

@INPROCEEDINGS{BABOOMS_ICRA_15, 
author = "{A. Bircher, K. Alexis, M. Burri, P. Oettershagen, S. Omari, T. Mantel and R. Siegwart}",
booktitle = {Robotics and Automation (ICRA), 2015 IEEE International Conference on}, 
title={Structural Inspection Path Planning via Iterative Viewpoint Resampling with Application to Aerial Robotics},
year={2015}, 
month={May}, 
pages={6423-6430}, 
}

Credits:

This algorithm was developed by Andreas Bircher with the help and support of the members of the Autonomous Systems Lab. The work was supported by the European Commission-funded projects AEROWORKS and ICARUS.

Contact:

You can contact us for any question or remark:
* Andreas Bircher
* Kostas Alexis