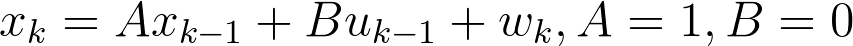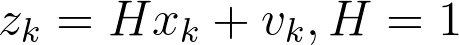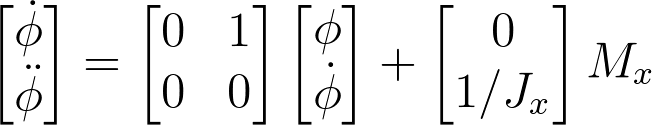Homework Assignments
Homework #1: Summarizing and presenting sections of a Book Chapter
Study the following chapter:
Stefan Leutenegger, Christoph Hürzeler, Amanda K. Stowers, Kostas Alexis, Markus W. Achtelik, David Lentink, Paul Y. Oh, Roland Siegwart, "Flying Robots", Handbook of Robotics, 2nd version
By summarizing any of the sections 26.3-26.6 and making a relevant ~10-slides presentation you can get a 5% grade improvement.
By summarizing any two of the sections 26.3-26.6 and making a relevant ~20-slides presentation you can get a 7.5% grade improvement.
Form of the Report: 1. Brief presentation overviewing the relevant topics. Presentation to take place in class.
Deadline: November 2, 2019
Form of Report: Please send the presentation file.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A2] NAME SURNAME"
Download the book chapter
Download presentation template
Study the following chapter:
Stefan Leutenegger, Christoph Hürzeler, Amanda K. Stowers, Kostas Alexis, Markus W. Achtelik, David Lentink, Paul Y. Oh, Roland Siegwart, "Flying Robots", Handbook of Robotics, 2nd version
By summarizing any of the sections 26.3-26.6 and making a relevant ~10-slides presentation you can get a 5% grade improvement.
By summarizing any two of the sections 26.3-26.6 and making a relevant ~20-slides presentation you can get a 7.5% grade improvement.
Form of the Report: 1. Brief presentation overviewing the relevant topics. Presentation to take place in class.
Deadline: November 2, 2019
Form of Report: Please send the presentation file.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A2] NAME SURNAME"
Download the book chapter
Download presentation template
Homework #2: Estimating a Random Constant
The goal of this task is to estimate a scalar random constant, which may be a voltage level. Let's assume that we have the ability to take measurements of the constant, but that the measurements are corrupted by 0.1 Volt RMS white measurement noise (e.g. our analog to digital converter is not very accurate). In this example, the process is governed by the linear difference equation:
The goal of this task is to estimate a scalar random constant, which may be a voltage level. Let's assume that we have the ability to take measurements of the constant, but that the measurements are corrupted by 0.1 Volt RMS white measurement noise (e.g. our analog to digital converter is not very accurate). In this example, the process is governed by the linear difference equation:
with a measurement z that is:
The state does not change from step to step, this is why A=1. There is no control input, therefore B =0,u=0. Our noisy measurement, directly measures the state - therefore H=1. Notice that the subscript k was dropped in several places because the respective parameters remain constant in our simple model.
Programming Language: preferably one Python, MATLAB, C++, or JAVA
Form of the Report: 1. Brief report with the code and the relevant plots indicating the correct estimate of the constant, 2. Comments on what you understood about the filter operation.
Deadline: November 20, 2019
Form of Report: Please send your code and an example of its execution in a pdf or other format.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A2] NAME SURNAME"
Help with the assignment: Please read the document "An Introduction to Kalman Flter" by Greg Welch and Gary Bishop. The assignment is the problem in Section 3 of this document.
Programming Language: preferably one Python, MATLAB, C++, or JAVA
Form of the Report: 1. Brief report with the code and the relevant plots indicating the correct estimate of the constant, 2. Comments on what you understood about the filter operation.
Deadline: November 20, 2019
Form of Report: Please send your code and an example of its execution in a pdf or other format.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A2] NAME SURNAME"
Help with the assignment: Please read the document "An Introduction to Kalman Flter" by Greg Welch and Gary Bishop. The assignment is the problem in Section 3 of this document.
Homework #2 - Bonus: Develop an EKF to estimate the attitude of the UAV based on its IMU data
|
Use the IMU data that you can download following this URL, and develop an Extended Kalman Filter solution to estimate the attitude of the aerial robot. For your development you can use any of the following languages: C++, Python, MATLAB Note that the data are available in the form of a ROS bag. The IMU data are collected using the VI-Sensor on-board the Firefly MAV. ROSBAG with IMU Data: Download Programming Language: C++, Python, MATLAB Deadline: November 20, 2019 Form of Report: Please send your code and a ROS bag with the new topics available. Alternatively, send your code and a *.csv or relevant file with the estimates. Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR BONUS2] NAME SURNAME" |
Homework #3: Studying a Research Paper
Study the following paper:
AJ Davison, "Real-Time Simultaneous Localisation and Mapping with a Single Camera"
And prepare an extended summary (2pages) as well as ~10slides presentation per team.
Deadline: December 2, 2019
Form of Report: Please prepare a presentation and extended notes. You will present during the weekly meeting.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A3] NAME SURNAME"
Download the paper
Download presentation template
Study the following paper:
AJ Davison, "Real-Time Simultaneous Localisation and Mapping with a Single Camera"
And prepare an extended summary (2pages) as well as ~10slides presentation per team.
Deadline: December 2, 2019
Form of Report: Please prepare a presentation and extended notes. You will present during the weekly meeting.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A3] NAME SURNAME"
Download the paper
Download presentation template
Homework #4: Control Design
For the linearized roll dynamics presented below:
For the linearized roll dynamics presented below:
Design a controller that ensures the stability of the system. Further provide a counter example. Argue about your design symbolically (no need for specific numbers - derive the expression for the poles or eigenvalues).
Deadline: December 5, 2019
Form of Report: Please prepare a written report
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A4] NAME SURNAME"
Deadline: December 5, 2019
Form of Report: Please prepare a written report
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A4] NAME SURNAME"
Homework #5 - Bonus: Develop a Python Model of a 2D Bicopter
Use Python and the ipython notebooks to create an interactive model of a 2D Bicopter such as the one shown below. Provide the ability to change mass, inertial and PID Control Gains in order to observe the attitude and position control response of the system.
States to be controlled: x position, velocity along x, pitch, pitch rate.
Control inputs: Thrust of Motor 1 and Thrust of Motor 2.
Deadline: December 10, 2019
Form of Report: Please prepare the *.ipynb notebook.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A5] NAME SURNAME"
Use Python and the ipython notebooks to create an interactive model of a 2D Bicopter such as the one shown below. Provide the ability to change mass, inertial and PID Control Gains in order to observe the attitude and position control response of the system.
States to be controlled: x position, velocity along x, pitch, pitch rate.
Control inputs: Thrust of Motor 1 and Thrust of Motor 2.
Deadline: December 10, 2019
Form of Report: Please prepare the *.ipynb notebook.
Submit your Report: Please send an e-mail to [email protected] and give it the following title "[IAR A5] NAME SURNAME"