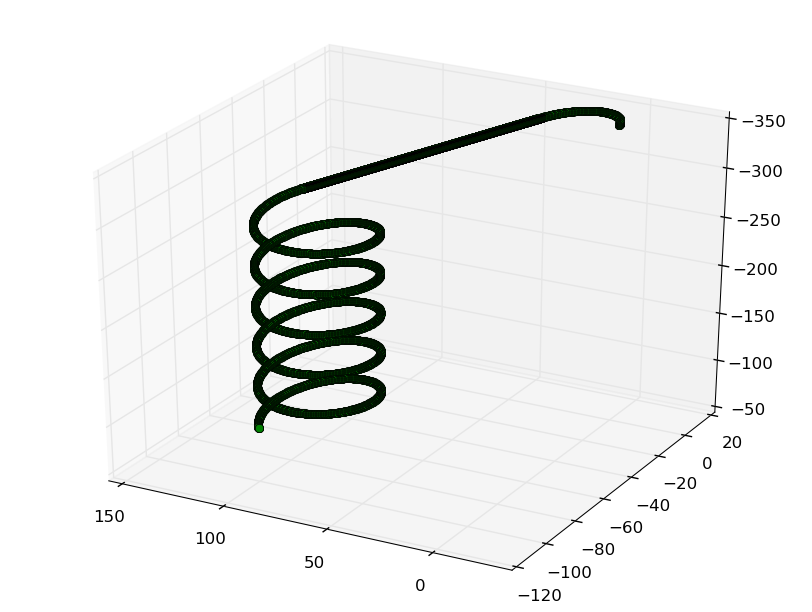
Dubins Airplane
Dubins airplane is an extension of the classical Dubins car model for the 3D case of an airplane. The specific implementation provided here relies on the formulation presented in:
(b)Mark Owen, Randal W. Beard and Timothy W. McLain, “Implementing Dubins Airplane Paths on Fixed-Wing UAVs”
and essentially (as described in this paper) corresponds to a modification of the initial model proposed by Lavalle et al. so that it becomes more consistent with the kinematics of a fixed-wing aircraft. Dubins airplane paths are more complicated than Dubins car paths because of the altitude component. Based on the difference between the altitude of the initial and final configurations, Dubins airplane paths can be classified as low, medium, or high altitude gain. While for medium and high altitude gain there are many different Dubins airplane paths, this implementation selects the pat that maximizes the average altitude throughout the maneuver.
Provided Implementations
1. Python
Run the example script “DubinsAirplaneMain.py” in which, one of the 16 supported path-cases may be found (parameter dubins_case):
python DubinsAirplaneMain.py
In the same file, the filename to save the path result (fname) can be edited while flags related with plotting (plot_flag) and execution verbosity (verbose_flag) can be set. Furthermore, the vehicle and mission-specific parameters:
* Vairspeed_0: nominal airspeed
* Bank_max: maximum banki angle
* Gamma_max: maximum flight path angle
should be modified.
or have a quick look to it below.
Dubins Airplane Implementation
# __DUBINSAIRPLANEMAIN__ # This is the main file to execute examples of the Dubins Airplane mode # that supports 16 cases of possible trajectories # # Authors: # Kostas Alexis ([email protected]) from DubinsAirplaneFunctions import * from PlottingTools import plot3 import numpy as np import time import sys pi = np.pi dubins_case = 0 verbose_flag = 0 plot_flag = 1 class ExecutionFlags(object): """ Execution flags """ def __init__(self, verbose_flag, plot_flag): self.verbose = verbose_flag self.plot = plot_flag class VehicleParameters(object): """ Vehicle Parameters """ def __init__(self, Vairspeed_0, Bank_max, Gamma_max): self.Vairspeed_0 = Vairspeed_0 self.Bank_max = Bank_max self.Gamma_max = Gamma_max def main(): # Example main for the 16 cases Dubins Airplane paths t0 = time.clock() VehiclePars = VehicleParameters( 15, pi/4, pi/6 ) ExFlags = ExecutionFlags( verbose_flag,plot_flag ) flag_nc = 0 fname = 'path_dubins_solution.txt' if dubins_case == 1: # short climb RSR print '### Path Type: short climb RSR' start_node = np.array( [0, 0, -100, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [0, 200, -125, 270*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 2: # short climb RSL print '### Path Type: short climb RSL' start_node = np.array([ 0, 0, -100, -70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, 100, -125, -70*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 3: # short climb LSR print '### Path Type: short climb LSR' start_node = np.array( [0, 0, -100, 70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -125, 70*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 4: # short climb LSL print '### Path Type: short climb LSL' start_node = np.array( [0, 0, -100, 70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -125, -135*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 5: # long climb RSR print '### Path Type: long climb RSR' start_node = np.array( [0, 0, -100, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [0, 200, -250, 270*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 6: # long climb RSL print '### Path Type: long climb RSL' start_node = np.array( [0, 0, -100, -70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, 100, -350, -70*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 7: # long climb LSR print '### Path Type: long climb LSR' start_node = np.array( [0, 0, -350, 70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -100, 70*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 8: # long climb LSL print '### Path Type: long climb LSL' start_node = np.array( [0, 0, -350, 70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -100, -135*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 9: # intermediate climb RLSR (climb at beginning) print '### Path Type: intermediate climb RLSR (climb at beginning)' start_node = np.array( [0, 0, -100, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [0, 200, -200, 270*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 10: # intermediate climb RLSL (climb at beginning) print '### Path Type: intermediate climb RLSL (climb at beginning)' start_node = np.array( [0, 0, -100, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, 100, -200, -90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 11: # intermediate climb LRSR (climb at beginning) print '### Path Type: intermediate climb LRSR (climb at beginning)' start_node = np.array( [0, 0, -100, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -200, 90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 12: # intermediate climb LRSL (climb at beginning) print '### Path Type: intermediate climb LRSL (climb at beginning)' start_node = np.array( [0, 0, -100, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -200, -90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 13: # intermediate climb RSLR (descend at end) print '### Path Type: intermediate climb RSLR (descend at end)' start_node = np.array( [0, 0, -200, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, 100, -100, 90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 14: # intermediate climb RSRL (descend at end) print '### Path Type: intermediate climb RSRL (descend at end)' start_node = np.array( [0, 0, -200, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, 100, -100, -90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 15: # intermediate climb LSLR (descend at end) print '### Path Type: intermediate climb LSLR (descend at end)' start_node = np.array( [0, 0, -200, 70*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100, -100, 90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 16: # intermediate climb LSRL (descend at end) print '### Path Type: intermediate climb LSRL (descend at end)' start_node = np.array( [0, 0, -150, 0*pi/180, VehiclePars.Vairspeed_0] ) end_node = np.array( [100, -100,-100, -90*pi/180, VehiclePars.Vairspeed_0] ) elif dubins_case == 0: # for fixing errors print '### Path Type: for fixing errors' start_node = np.array( [0, 0, 0, 0, VehiclePars.Vairspeed_0] ) end_node = np.array( [40, -140, 100, 11*pi/9, VehiclePars.Vairspeed_0] ) # LSRL #end_node = np.array( [40, -140, 140, 2*pi/9, VehiclePars.Vairspeed_0] ) # LSLR #end_node = np.array( [40, 140, 140, 11*pi/9, VehiclePars.Vairspeed_0] ) # RSLR #end_node = np.array( [40, 140, 140, 1*pi/9, VehiclePars.Vairspeed_0] ) # RSRL #end_node = np.array( [40, 140, -140, 11*pi/9, VehiclePars.Vairspeed_0] ) # RLSR end_node = np.array( [60, 140, -140, 0*pi/14, VehiclePars.Vairspeed_0] ) # RLSL #end_node = np.array( [40, -140, -100, 11*pi/9, VehiclePars.Vairspeed_0] ) # LRSL end_node = np.array( [40, -140, -100, 10*pi/180, VehiclePars.Vairspeed_0] ) # LRSR if dubins_case > 16: flag_nc = 1 print 'Not a case' if flag_nc == 0: print '### Case loaded.' print '### computing path...' R_min = MinTurnRadius_DubinsAirplane( VehiclePars.Vairspeed_0, VehiclePars.Bank_max ) # Check if start and end node are too close. Since spiral-spiral-spiral (or curve-curve-curve) paths are not considered, the optimal path may not be found... (see Shkel, Lumelsky, 2001, Classification of the Dubins set, Prop. 5/6). Below is a conservative bound, which seems (by experiments) to assure a unproblematical computation of the dubins path. if ( np.linalg.norm(end_node[0:2] - start_node[0:2],ord=2) < 6*R_min ): print "!!!!!!!!!!!!!!!!" print "Conservative condition (end_node[0:2] - start_node[0:2],ord=2) < 6*R_min) not fulfilled!" print "Start and end pose are close together. Path of type RLR, LRL may be optimal" print "May fail to compute optimal path! Aborting" print "!!!!!!!!!!!!!!!!" sys.exit() DubinsAirplaneSolution = DubinsAirplanePath( start_node, end_node, R_min, VehiclePars.Gamma_max ) if ExFlags.verbose : PrintSolutionAgainstMATLAB( DubinsAirplaneSolution ) path_dubins_airplane = ExtractDubinsAirplanePath( DubinsAirplaneSolution ) path_dubins_airplane = path_dubins_airplane.T print '### Execution time = ' + str( time.clock() - t0 ) np.savetxt( fname, path_dubins_airplane.T, delimiter = ',' ) print '### Dubins airplane solution saved in ' + fname if ExFlags.plot : print '### Dubins airplane solution plot' plot3( path_dubins_airplane[:,0], path_dubins_airplane[:,1], path_dubins_airplane[:,2], 'o', 'g' ) # print 'Press any button to continue' # raw_input() def testAllCases(): #for dubins_case in xrange(1, 16): main() print 'Press any button to continue' raw_input() if __name__ == "__main__": testAllCases()
# __DUBINSAIRPLANEFUNCTIONS__ # The functions here implement the 3D Dubins Airplane model with totally # 16 cases of possible trajectories # # Authors: # Kostas Alexis ([email protected]) from __future__ import division import numpy as np from math import tan, sin, cos, atan2, fmod, acos, asin, pow, sqrt, fabs,atan from ElementaryFunctions import max, min pi = np.pi # create the results dictionary DubinsAirplaneSolution = { } DubinsAirplaneSolution['case'] = 0 DubinsAirplaneSolution['p_s'] = np.zeros((3,1)) DubinsAirplaneSolution['angl_s'] = 0 DubinsAirplaneSolution['p_e'] = np.zeros((3,1)) DubinsAirplaneSolution['R'] = 0 DubinsAirplaneSolution['gamma'] = 0 DubinsAirplaneSolution['L'] = 0 DubinsAirplaneSolution['c_s'] = np.zeros((3,1)) DubinsAirplaneSolution['psi_s'] = 0 DubinsAirplaneSolution['lamda_s'] = 0 DubinsAirplaneSolution['lamda_si'] = 0 DubinsAirplaneSolution['k_s'] = 0 DubinsAirplaneSolution['c_ei'] = np.zeros((3,1)) DubinsAirplaneSolution['c_si'] = np.zeros((3,1)) DubinsAirplaneSolution['psi_ei'] = 0 DubinsAirplaneSolution['lamda_ei'] = 0 DubinsAirplaneSolution['psi_si'] = 0 DubinsAirplaneSolution['k_ei'] = 0 DubinsAirplaneSolution['c_e'] = 0 DubinsAirplaneSolution['k_si'] = 0 DubinsAirplaneSolution['psi_e'] = 0 DubinsAirplaneSolution['lamda_e'] = 0 DubinsAirplaneSolution['k_e'] = 0 DubinsAirplaneSolution['w_s'] = np.zeros((3,1)) DubinsAirplaneSolution['q_s'] = np.zeros((3,1)) DubinsAirplaneSolution['w_si'] = np.zeros((3,1)) DubinsAirplaneSolution['q_si'] = np.zeros((3,1)) DubinsAirplaneSolution['w_l'] = np.zeros((3,1)) DubinsAirplaneSolution['q_l'] = np.zeros((3,1)) DubinsAirplaneSolution['w_ei'] = np.zeros((3,1)) DubinsAirplaneSolution['q_ei'] = np.zeros((3,1)) DubinsAirplaneSolution['w_e'] = np.zeros((3,1)) DubinsAirplaneSolution['q_e'] = np.zeros((3,1)) def roty(theta=None): # Rotation around y R = np.array([ [cos(theta), 0, sin(theta)], [0, 1, 0], [-sin(theta), 0, cos(theta)] ]) return R def rotz(theta=None): # Rotation around z R = np.array([ [cos(theta), -sin(theta), 0], [sin(theta), cos(theta), 0], [0, 0, 1] ]) return R def computeDubinsRSR(R=None, crs=None, cre=None, anglstart=None,anglend=None): # Compute Dubins RSR theta = atan2( cre[1]-crs[1], cre[0]-crs[0] ) L = np.linalg.norm( crs[0:2]-cre[0:2],ord=2 ) + R* fmod( 2*pi+fmod(theta-pi/2,2*pi )-fmod( anglstart-pi/2,2*pi),2*pi ) + R*fmod( 2*pi+fmod(anglend-pi/2,2*pi )-fmod( theta-pi/2,2*pi),2*pi ) return L def computeDubinsLSL(R=None, cls=None, cle=None, anglstart=None, anglend=None): # Compute Dubins LSL theta = atan2( cle[1]-cls[1], cle[0]-cls[0] ) L = np.linalg.norm(cls[0:2]-cle[0:2]) + R*fmod( 2*pi-fmod(theta+pi/2,2*pi)+fmod(anglstart+pi/2,2*pi),2*pi ) + R*fmod( 2*pi-fmod(anglend+pi/2,2*pi)+fmod(theta+pi/2,2*pi),2*pi ) return L def computeDubinsLSR(R=None, cls=None, cre=None, anglstart=None, anglend=None): # Compute Dubins LSR ell = np.linalg.norm( cre[0:2]-cls[0:2],ord=2 ) theta = atan2( cre[1]-cls[1],cre[0]-cls[0] ) acos_value = 2 * R / ell if fabs( acos_value ) > 1: flag_zero = 1 else: flag_zero = 0 acos_value = max( acos_value,-1 ) acos_value = min( acos_value,1 ) if ell == 0: theta2 = 0 else: theta2 = acos( acos_value ) if flag_zero == 1: theta2 = 0 if theta2 == 0: L = pow(10.0,8) else: L = sqrt( pow(ell,2) - 4*pow(R,2) ) + R*fmod( 2*pi-fmod(theta+theta2,2*pi ) + fmod( anglstart+pi/2,2*pi),2*pi ) + R*fmod( 2*pi-fmod(theta+theta2-pi,2*pi)+fmod(anglend-pi/2,2*pi),2*pi ) return L def computeDubinsRSL(R=None, crs=None, cle=None, anglstart=None, anglend=None): # Compute Dubins RSL ell = np.linalg.norm( cle[0:2]-crs[0:2],ord=2 ) theta = atan2( cle[1]-crs[1],cle[0]-crs[0] ) asin_value = 2 * R / ell if fabs( asin_value ) > 1: flag_zero = 1 else: flag_zero = 0 asin_value = max( asin_value, -1 ) asin_value = min( asin_value, 1 ) if ell == 0: theta2 = 0 else: theta2 = theta - pi/2 + asin( asin_value ) if theta2 == 0: L = pow( 10.0, 8 ) else: L = sqrt( fabs(pow(ell,2)-4 * pow(R,2)) ) + R * fmod( 2 * pi + fmod( theta2, 2 * pi )-fmod( anglstart-pi/2, 2 * pi ), 2 * pi ) + R * fmod( 2 * pi + fmod( theta2 + pi, 2 * pi )-fmod( anglend + pi / 2, 2 * pi ), 2 * pi ) return L def computeOptimalRadius(zs=None, anglstart=None, ze=None, anglend=None, R_min=None, gamma_max=None, idx=None, k=None, hdist=None): # Compute Optimal Radius R1 = R_min R2 = 2 * R_min R = ( R1 + R2 ) / 2 if idx == 1: error = 1 while fabs( error ) > 0.1: crs = zs + R * np.dot( rotz( pi / 2 ),np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R * np.dot( rotz( pi / 2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsRSR(R, crs, cre, anglstart, anglend) error = ( L + 2 * pi * k * R ) - fabs( hdist ) / tan( gamma_max ) if error > 0: R2 = R else: R1 = R R= ( R1 + R2 ) / 2 elif idx == 2: error = 1 while fabs( error ) > 0.1: crs = zs + R * np.dot( rotz( pi / 2 ),np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cle = ze + R * np.dot( rotz( -pi/2 ),np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsRSL( R, crs, cle, anglstart, anglend ) error = ( L + 2 * pi * k * R ) * tan( gamma_max ) - fabs( hdist ) if error > 0: R2 = R else: R1 = R R = ( R1 + R2 ) / 2 elif idx == 3: error = 1 while fabs( error ) > 0.1: cls = zs + R * np.dot( rotz( -pi / 2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R * np.dot( rotz( pi / 2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsLSR( R, cls, cre, anglstart, anglend ) error = ( L + 2 * pi * k * R ) * tan( gamma_max ) - fabs( hdist ) if error > 0: R2 = R else: R1 = R R = ( R1 + R2 ) / 2 elif idx == 4: error = 1 while fabs( error ) > 0.1: cls = zs + R * np.dot( rotz( -pi / 2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cle = ze + R * np.dot( rotz( -pi / 2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsLSL( R, cls, cle, anglstart, anglend ) error = ( L + 2 * pi * k * R ) * tan( gamma_max ) - fabs( hdist ) if error > 0: R2 = R else: R1 = R R = ( R1 + R2 ) / 2 return R def MinTurnRadius_DubinsAirplane(V=None,phi_max=None): # Compute Minimum Turning Radius g = 9.8065 Rmin = pow( V,2 ) / (g * tan( phi_max ) ) return Rmin def addSpiralBeginning(zs=None, anglstart=None, ze=None, anglend=None, R_min=None, gamma_max=None, idx=None, hdist=None): # Add Spiral in the Dubins Airplane Path beginning cli = np.zeros((3,1)) cri = np.zeros((3,1)) zi = np.zeros((3,1)) anglinter = 0 L = 0 ci = np.zeros((3,1)) psii = 0 psi1 = 0 psi2 = 2 * pi psi = ( psi1 + psi2 ) / 2 if idx == 1: # RLSR crs = zs + R_min * np.dot( rotz( pi/2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R_min * np.dot( rotz( pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsRSR( R_min, crs, cre, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = crs + np.dot( rotz( psi ),( zs-crs ) ) anglinter = anglstart + psi cli = zi + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsLSR( R_min, cli, cre, anglinter, anglend ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = crs + np.dot( rotz( psi ), ( zs-crs ) ) anglinter = anglstart + psi L = L + fabs( psi ) * R_min ci = cli psii = psi elif idx == 2: # RLSL crs = zs + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cle = ze + R_min * np.dot( rotz( -pi / 2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsRSL( R_min, crs, cle, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = crs + np.dot( rotz( psi ), ( zs-crs ) ) anglinter = anglstart + psi cli = zi + R_min * np.dot( rotz( -pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsLSL( R_min, cli, cle, anglinter, anglend ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = crs + np.dot( rotz( psi ), ( zs-crs ) ) anglinter = anglstart + psi L = L + fabs( psi ) * R_min ci = cli psii = psi elif idx == 3: # LRSR cls = zs + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R_min * np.dot( rotz( pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsLSR( R_min, cls, cre, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = cls + np.dot( rotz( -psi ), ( zs-cls ) ) anglinter = anglstart - psi cri = zi + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsRSR( R_min, cri, cre, anglinter, anglend ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = cls + np.dot( rotz( -psi ), ( zs-cls ) ) anglinter = anglstart - psi L = L + fabs( psi ) * R_min ci = cri psii = psi elif idx == 4: # LRSL cls = zs + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cle = ze + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) # above modified by liucz 2015-10-12, fix spell mistake cre -> cle # origin is "cre = ze + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T )" L = computeDubinsLSL( R_min, cls, cle, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = cls + np.dot( rotz( -psi ), ( zs-cls ) ) anglinter = anglstart - psi cri = zi + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0 ] ).T ) # above is modified by licz 2015-10-12, fix written mistake np.array -> np.dot # origin is "cri = zi + R_min * np.array( rotz( pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0 ] ).T )" L = computeDubinsRSL( R_min, cri, cle, anglinter, anglend ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = cls + np.dot( rotz( -psi ), ( zs-cls ) ) anglinter = anglstart - psi L = L + fabs( psi ) * R_min ci = cri psii = psi return zi, anglinter, L, ci, psii def addSpiralEnd(zs=None, anglstart=None, ze=None, anglend=None, R_min=None, gamma_max=None, idx=None, hdist=None): # Add Spiral at the end of the Dubins Airplane path cli = np.zeros((3,1)) cri = np.zeros((3,1)) zi = np.zeros((3,1)) anglinter = 0 L = 0 ci = np.zeros((3,1)) psii = 0 psi1 = 0 psi2 = 2 * pi psi = ( psi1 + psi2 ) / 2 if idx == 1: # RSLR crs = zs + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R_min * np.dot( rotz( pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsRSR( R_min, crs, cre, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = cre + np.dot( rotz( -psi ), ( ze-cre ) ) anglinter = anglend - psi cli = zi + R_min * np.dot( rotz( -pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsRSL( R_min, crs, cli, anglstart, anglinter ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = cre + np.dot( rotz( -psi ), ( ze-cre ) ) anglinter = anglend - psi L = L + abs( psi ) * R_min ci = cli psii = psi elif idx == 2: # RSRL crs = zs + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cle = ze + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsRSL( R_min, crs, cle, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = cle + np.dot( rotz( psi ), ( ze-cle ) ) anglinter = anglend + psi cri = zi + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsRSR( R_min, crs, cri, anglstart, anglinter ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = cle + np.dot( rotz( psi ), ( ze-cle ) ) anglinter = anglend + psi cri = zi + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = L + fabs( psi ) * R_min ci = cri psii = psi elif idx == 3: # LSLR cls = zs + R_min * np.dot( rotz( -pi / 2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsLSR( R_min, cls, cre, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max )) while fabs( error ) > 0.001: zi = cre + np.dot( rotz( -psi ), ( ze-cre ) ) anglinter = anglend - psi cli = zi + R_min * np.dot( rotz( -pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsLSL( R_min, cls, cli, anglstart, anglinter ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = cre + np.dot( rotz( -psi ), ( ze-cre ) ) anglinter = anglend - psi L = L + fabs( psi ) * R_min ci = cli psii = psi elif idx == 4: cls = zs + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cle = ze + R_min * np.dot( rotz( -pi/2 ), np.array( [cos(anglend), sin(anglend), 0] ).T ) L = computeDubinsLSL( R_min, cls, cle, anglstart, anglend ) error = L - fabs( hdist / tan( gamma_max ) ) while fabs( error ) > 0.001: zi = cle + np.dot( rotz( psi ), ( ze-cle ) ) anglinter = anglend + psi cri = zi + R_min * np.dot( rotz( pi / 2 ), np.array( [cos(anglinter), sin(anglinter), 0] ).T ) L = computeDubinsLSR( R_min, cls, cri, anglstart, anglinter ) error = ( L + fabs( psi ) * R_min ) - fabs( hdist / tan( gamma_max ) ) if error > 0: psi2 = (179*psi2+psi)/180 else: psi1 = (179*psi1+psi)/180 psi = ( psi1 + psi2 ) / 2 zi = cle + np.dot( rotz( psi ), ( ze-cle )) anglinter = anglend + psi L = L + fabs( psi ) * R_min ci = cri psii = psi return zi, anglinter, L, ci, psii def DubinsAirplanePath(init_conf=None, final_conf=None, R_min=None, gamma_max=None): # Compute the Dubins Airplane path zs = (init_conf[0:3]).T anglstart = init_conf[3] ze = (final_conf[0:3]).T anglend = final_conf[3] DubinsAirplaneSolution['p_s'] = zs DubinsAirplaneSolution['angl_s'] = anglstart DubinsAirplaneSolution['p_e'] = ze DubinsAirplaneSolution['angl_e'] = anglend crs = zs + R_min*np.dot(rotz(pi/2), np.array([cos(anglstart), sin(anglstart), 0]).T) cls = zs + R_min*np.dot(rotz(-pi/2),np.array([cos(anglstart), sin(anglstart), 0]).T) cre = ze + R_min*np.dot(rotz(pi/2),np.array([cos(anglend), sin(anglend), 0]).T) cle = ze + R_min*np.dot(rotz(-pi/2),np.array([cos(anglend), sin(anglend), 0]).T) # compute L1, L2, L3, L4 L1 = computeDubinsRSR(R_min, crs, cre, anglstart, anglend) L2 = computeDubinsRSL(R_min, crs, cle, anglstart, anglend) L3 = computeDubinsLSR(R_min, cls, cre, anglstart, anglend) L4 = computeDubinsLSL(R_min, cls, cle, anglstart, anglend) # L is the minimum distance L = np.amin(np.array([L1, L2, L3, L4])) idx = np.where(np.array([L1,L2,L3,L4])==L)[0][0] + 1 hdist = -(ze[2] - zs[2]) if fabs(hdist) <= L*tan(gamma_max): gam = atan(hdist/L) DubinsAirplaneSolution['case'] = 1 DubinsAirplaneSolution['R'] = R_min DubinsAirplaneSolution['gamma'] = gam DubinsAirplaneSolution['L'] = L/cos(gam) DubinsAirplaneSolution['k_s'] = 0 DubinsAirplaneSolution['k_e'] = 0 elif fabs(hdist) >= (L+2*pi*R_min)*tan(gamma_max): k = np.floor( (fabs(hdist)/tan(gamma_max) - L)/(2*pi*R_min)) if hdist >= 0: DubinsAirplaneSolution['k_s'] = k DubinsAirplaneSolution['k_e'] = 0 else: DubinsAirplaneSolution['k_s'] = 0 DubinsAirplaneSolution['k_e'] = k # find optimal turning radius R = computeOptimalRadius(zs, anglstart, ze, anglend, R_min, gamma_max, idx, k, hdist) # recompute the centers of spirals and Dubins path length with new R crs = zs + R*np.dot(rotz(pi/2), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cls = zs + R*np.dot(rotz(-pi/2), np.array( [cos(anglstart), sin(anglstart), 0] ).T ) cre = ze + R*np.dot(rotz(pi/2), np.array( [cos(anglend), sin(anglend), 0] ).T ) cle = ze + R*np.dot(rotz(-pi/2), np.array( [cos(anglend), sin(anglend), 0] ).T ) if idx == 1: L = computeDubinsRSR( R, crs, cre, anglstart, anglend ) elif idx == 2: L = computeDubinsRSL( R, crs, cle, anglstart, anglend ) elif idx == 3: L = computeDubinsLSR( R, cls, cre, anglstart, anglend ) elif idx == 4: L = computeDubinsLSL( R, cls, cle, anglstart, anglend ) DubinsAirplaneSolution['case'] = 1 DubinsAirplaneSolution['R'] = R gam = np.sign( hdist ) * gamma_max DubinsAirplaneSolution['gamma'] = gam DubinsAirplaneSolution['L'] = ( L + 2 * pi * k * R ) / cos( gamma_max ) else: gam = np.sign( hdist ) * gamma_max if hdist > 0: zi, chii, L, ci, psii = addSpiralBeginning( zs, anglstart, ze, anglend, R_min, gam, idx, hdist ) DubinsAirplaneSolution['case'] = 2 else: zi, chii, L, ci, psii = addSpiralEnd( zs, anglstart, ze, anglend, R_min, gam, idx, hdist ) DubinsAirplaneSolution['case'] = 3 DubinsAirplaneSolution['R'] = R_min DubinsAirplaneSolution['gamma'] = gam DubinsAirplaneSolution['L'] = L / cos( gamma_max ) e1 = np.array( [1, 0, 0] ).T R = DubinsAirplaneSolution['R'] if np.isscalar(DubinsAirplaneSolution['case']): pass else: print '### Error' if DubinsAirplaneSolution['case'] == 1: # spiral-line-spiral if idx == 1: # right-straight-right theta = atan2( cre[1]-crs[1], cre[0]-crs[0]) dist1 = R*fmod(2*pi+fmod(theta-pi/2,2*pi)-fmod(anglstart-pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_s'] dist2 = R*fmod(2*pi+fmod(anglend-pi/2,2*pi)-fmod(theta-pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_e'] w1 = crs + DubinsAirplaneSolution['R']*np.dot(rotz(theta-pi/2),e1.T).T + np.array([0,0,-dist1*tan(gam)]).T w2 = cre + DubinsAirplaneSolution['R']*np.dot(rotz(theta-pi/2),e1.T).T - np.array([0,0,-dist2*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # direction of line DubinsAirplaneSolution['c_s'] = crs DubinsAirplaneSolution['psi_s'] = anglstart-pi/2 DubinsAirplaneSolution['lamda_s'] = 1 # end spiral DubinsAirplaneSolution['c_e'] = cre-np.array([0,0,-dist2*tan(gam)]) DubinsAirplaneSolution['psi_e'] = theta-pi/2 DubinsAirplaneSolution['lamda_e'] = 1 # hyperplane H_s: switch from first spiral to line DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from line to last spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1,0,0]).T) elif idx == 2: # right-straight-left ell = np.linalg.norm(cle[0:2] - crs[0:2],ord=2) theta = atan2(cle[1]-crs[1], cle[0]-crs[0]) theta2 = theta - pi/2 + asin(2*R/ell) dist1 = R*fmod(2*pi+fmod(theta2,2*pi)-fmod(anglstart-pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_s'] dist2 = R*fmod(2*pi+fmod(theta2+pi,2*pi)-fmod(anglend+pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_e'] w1 = crs + R*np.dot(rotz(theta2), e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = cle + R*np.dot(rotz(theta2+pi),e1.T).T - np.array([0,0,-dist2*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = crs DubinsAirplaneSolution['psi_s'] = anglstart-pi/2 DubinsAirplaneSolution['lamda_s'] = 1 # end spiral DubinsAirplaneSolution['c_e'] = cle - np.array([0,0,-dist2*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = theta2+pi DubinsAirplaneSolution['lamda_e'] = -1 # hyperplane H_s: switch from first spiral to line DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend),np.array([1,0,0]).T) elif idx == 3: # left-straight-right ell = np.linalg.norm(cre[0:2]-cls[0:2],ord=2) theta = atan2( cre[1]-cls[1],cre[0]-cls[0]) theta2 = acos(2*R/ell) dist1 = R*fmod(2*pi-fmod(theta+theta2,2*pi) + fmod(anglstart+pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_s'] dist2 = R*fmod(2*pi-fmod(theta+theta2-pi,2*pi)+fmod(anglend-pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_e'] w1 = cls + R*np.dot(rotz(theta+theta2),e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = cre + R*np.dot(rotz(-pi+theta+theta2),e1.T).T - np.array([0, 0, -dist2*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = cls DubinsAirplaneSolution['psi_s'] = anglstart+pi/2 DubinsAirplaneSolution['lamda_s'] = -1 # end spiral DubinsAirplaneSolution['c_e'] = cre - np.array([0,0,-dist2*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = fmod(theta+theta2-pi,2*pi) DubinsAirplaneSolution['lamda_e'] = 1 # hyperplane H_s: switch from first spiral to line DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1, 0, 0]).T) elif idx ==4: # left-straight-left theta = atan2(cle[1] -cls[1], cle[0] - cls[0]) dist1 = R*fmod(2*pi-fmod(theta+pi/2,2*pi)+fmod(anglstart+pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_s'] dist2 = R*fmod(2*pi-fmod(anglend+pi/2,2*pi)+fmod(theta+pi/2,2*pi),2*pi) + 2*pi*R*DubinsAirplaneSolution['k_e'] w1 = cls + DubinsAirplaneSolution['R']*np.dot(rotz(theta+pi/2),e1.T).T + np.array([0,0,-dist1*tan(gam)]).T w2 = cle + DubinsAirplaneSolution['R']*np.dot(rotz(theta+pi/2),e1.T).T - np.array([0,0,-dist2*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = cls DubinsAirplaneSolution['psi_s'] = anglstart+pi/2 DubinsAirplaneSolution['lamda_s'] = -1 # end spiral DubinsAirplaneSolution['c_e'] = cle - np.array([0,0,-dist2*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = theta+pi/2 DubinsAirplaneSolution['lamda_e'] = -1 # hyperplane H_s: switch from first spiral to line DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1,0,0]).T) elif DubinsAirplaneSolution['case'] == 2: if idx == 1: # right-left-straight-right # start spiral DubinsAirplaneSolution['c_s'] = crs DubinsAirplaneSolution['psi_s'] = anglstart-pi/2 DubinsAirplaneSolution['lamda_s'] = 1 DubinsAirplaneSolution['k_s'] = 0 ell = np.linalg.norm(cre[0:2]-ci[0:2],ord=2) theta = atan2(cre[1] - ci[1], cre[0] - ci[0]) theta2 = acos(2*R/ell) dist1 = R_min*psii + R*fmod(2*pi-fmod(theta+theta2,2*pi) + fmod(chii+pi/2,2*pi),2*pi) dist2 = R*fmod(2*pi-fmod(theta+theta2-pi,2*pi)+fmod(anglend-pi/2,2*pi),2*pi) w1 = ci + R*np.dot(rotz(theta+theta2),e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = cre + R*np.dot(rotz(-pi+theta+theta2),e1.T).T - np.array([0, 0, -dist2*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # intermediate-start spiral DubinsAirplaneSolution['c_si'] = ci + np.array([0, 0, -R_min*psii*tan(gam)]).T DubinsAirplaneSolution['psi_si'] = chii + pi/2 DubinsAirplaneSolution['lamda_si'] = -1 DubinsAirplaneSolution['k_si'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cre - np.array([0,0,-dist2*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = fmod(theta+theta2-pi,2*pi) DubinsAirplaneSolution['lamda_e'] = 1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = zi - np.array([0, 0, -psii*R_min*tan(gam)]).T DubinsAirplaneSolution['q_s'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_si: switch from second spiral to straight line DubinsAirplaneSolution['w_si'] = w1 DubinsAirplaneSolution['q_si'] = q1 # hyperplane H_l: switch from straight-line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1,0,0]).T) elif idx == 2: # right-left-straight-left theta = atan2(cle[1]-ci[1],cle[0]-ci[0]) dist1 = R*fmod(2*pi-fmod(theta+pi/2,2*pi)+fmod(chii+pi/2,2*pi),2*pi) dist2 = psii*R dist3 = R*fmod(2*pi-fmod(anglend+pi/2,2*pi)+fmod(theta+pi/2,2*pi),2*pi) w1 = ci + DubinsAirplaneSolution['R']*np.dot(rotz(theta+pi/2),e1.T).T + np.array([0, 0, -(dist1+dist2)*tan(gam)]).T w2 = cle + DubinsAirplaneSolution['R']*np.dot(rotz(theta+pi/2),e1.T).T - np.array([0,0,-dist3*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # direction of line # start spiral DubinsAirplaneSolution['c_s'] = crs DubinsAirplaneSolution['psi_s'] = anglstart-pi/2 DubinsAirplaneSolution['lamda_s'] = 1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-start spiral DubinsAirplaneSolution['c_si'] = ci + np.array([0, 0, -dist2*tan(gam)]).T DubinsAirplaneSolution['psi_si'] = chii+pi/2 DubinsAirplaneSolution['lamda_si'] = -1 DubinsAirplaneSolution['k_si'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cle - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = theta+pi/2 DubinsAirplaneSolution['lamda_e'] = -1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = zi - np.array([0, 0, -dist2*tan(gam)]).T DubinsAirplaneSolution['q_s'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_si: switch from second spiral to straight line DubinsAirplaneSolution['w_si'] = w1 DubinsAirplaneSolution['q_si'] = q1 # hyperplane H_l: switch from straight-line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1, 0, 0]).T) elif idx == 3: # left-right-straight-right theta = atan2(cre[1]-ci[1], cre[0] - ci[0]) dist1 = R*fmod(2*pi+fmod(theta-pi/2,2*pi)-fmod(chii-pi/2,2*pi),2*pi) dist2 = psii*R dist3 = R*fmod(2*pi+fmod(anglend-pi/2,2*pi)-fmod(theta-pi/2,2*pi),2*pi) w1 = ci + DubinsAirplaneSolution['R']*np.dot(rotz(theta-pi/2),e1.T).T + np.array([0, 0, -(dist1+dist2)*tan(gam)]).T w2 = cre + DubinsAirplaneSolution['R']*np.dot(rotz(theta-pi/2),e1.T).T - np.array([0, 0, -dist3*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # direction of line # start spiral DubinsAirplaneSolution['c_s'] = cls DubinsAirplaneSolution['psi_s'] = anglstart+pi/2 DubinsAirplaneSolution['lamda_s'] = -1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-start spiral DubinsAirplaneSolution['c_si'] = ci + np.array([0, 0, -dist2*tan(gam)]).T DubinsAirplaneSolution['psi_si'] = chii-pi/2 DubinsAirplaneSolution['lamda_si'] = 1 DubinsAirplaneSolution['k_si'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cre - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = theta-pi/2 DubinsAirplaneSolution['lamda_e'] = 1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = zi - np.array([0, 0, -dist2*tan(gam)]).T DubinsAirplaneSolution['q_s'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_si: switch from second spiral to straight line DubinsAirplaneSolution['w_si'] = w1 DubinsAirplaneSolution['q_si'] = q1 # hyperplane H_l: switch from straight-line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1,0,0]).T) elif idx == 4: # left-right-straight-left ell = np.linalg.norm(cle[0:2]-ci[0:2],ord=2) theta = atan2(cle[1] - ci[1], cle[0] - ci[0]) theta2 = theta - pi/2 + asin(2*R/ell) dist1 = R*fmod(2*pi+fmod(theta2,2*pi) - fmod(chii-pi/2,2*pi),2*pi) dist2 = R*psii dist3 = R*fmod(2*pi+fmod(theta2+pi,2*pi) - fmod(anglend+pi/2,2*pi),2*pi) w1 = ci + R*np.dot(rotz(theta2),e1.T).T + np.array([0, 0, -(dist1+dist2)*tan(gam)]).T w2 = cle + R*np.dot(rotz(theta2+pi),e1.T).T - np.array([0, 0, -dist3*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = cls DubinsAirplaneSolution['psi_s'] = anglstart+pi/2 DubinsAirplaneSolution['lamda_s'] = -1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-start spiral DubinsAirplaneSolution['c_si'] = ci + np.array([0, 0, -dist2*tan(gam)]).T DubinsAirplaneSolution['psi_si'] = chii-pi/2 DubinsAirplaneSolution['lamda_si'] = 1 DubinsAirplaneSolution['k_si'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cle - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = theta2+pi DubinsAirplaneSolution['lamda_e'] = -1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = zi - np.array([0, 0, -dist2*tan(gam)]).T DubinsAirplaneSolution['q_s'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_si: switch from second spiral to straight line DubinsAirplaneSolution['w_si'] = w1 DubinsAirplaneSolution['q_si'] = q1 # hyperplane H_l: switch from straight-line to end spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1, 0, 0]).T) elif DubinsAirplaneSolution['case'] == 3: if idx == 1: # right-straight-left-right # path specific calculations ell = np.linalg.norm(ci[0:2] - crs[0:2],ord=2) theta = atan2(ci[1] - crs[1], ci[0] - crs[0]) theta2 = theta-pi/2 + asin(2*R/ell) dist1 = R*fmod(2*pi+fmod(theta2,2*pi) - fmod(anglstart-pi/2,2*pi),2*pi) dist2 = R*fmod(2*pi+fmod(theta2+pi,2*pi)-fmod(chii+pi/2,2*pi),2*pi) dist3 = fabs(R_min*psii) w1 = crs + R*np.dot(rotz(theta2),e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = ci + R*np.dot(rotz(theta2+pi),e1.T).T - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = crs DubinsAirplaneSolution['psi_s'] = anglstart-pi/2 DubinsAirplaneSolution['lamda_s'] = 1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-end spiral DubinsAirplaneSolution['c_ei'] = ci - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T DubinsAirplaneSolution['psi_ei'] = theta2+pi DubinsAirplaneSolution['lamda_ei'] = -1 DubinsAirplaneSolution['k_ei'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cre - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = anglend-pi/2-psii DubinsAirplaneSolution['lamda_e'] = 1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from straight-line to intermediate spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_ei: switch from intermediate spiral to # end spiral DubinsAirplaneSolution['w_ei'] = zi - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['q_ei'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend),np.array([1,0,0]).T) elif idx == 2: # right-straight-right-left # path specific calculations theta = atan2(ci[1] - crs[1], ci[0] - crs[0]) dist1 = R*fmod(2*pi+fmod(theta-pi/2,2*pi) - fmod(anglstart-pi/2,2*pi),2*pi) dist2 = R*fmod(2*pi+fmod(chii-pi/2,2*pi) - fmod(theta-pi/2,2*pi),2*pi) dist3 = fabs(R_min*psii) w1 = crs + R*np.dot(rotz(theta-pi/2),e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = ci + R*np.dot(rotz(theta-pi/2),e1.T).T - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = crs DubinsAirplaneSolution['psi_s'] = anglstart-pi/2 DubinsAirplaneSolution['lamda_s'] = 1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-end spiral DubinsAirplaneSolution['c_ei'] = ci - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T DubinsAirplaneSolution['psi_ei'] = theta - pi/2 DubinsAirplaneSolution['lamda_ei'] = 1 DubinsAirplaneSolution['k_ei'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cle - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = anglend+pi/2+psii DubinsAirplaneSolution['lamda_e'] = -1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from straight-line to intermediate spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_ei: switch from intermediate spiral to # end spiral DubinsAirplaneSolution['w_ei'] = zi - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['q_ei'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1, 0, 0]).T) elif idx == 3: # left-straight-left-right # path specific calculations theta = atan2(ci[1]-cls[1],ci[0]-cls[0]) dist1 = R*fmod(2*pi-fmod(theta+pi/2,2*pi)+fmod(anglstart+pi/2,2*pi),2*pi) dist2 = R*fmod(2*pi-fmod(chii+pi/2,2*pi)+fmod(theta+pi/2,2*pi),2*pi) dist3 = fabs(R_min*psii) w1 = cls + DubinsAirplaneSolution['R']*np.dot(rotz(theta+pi/2),e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = ci + DubinsAirplaneSolution['R']*np.dot(rotz(theta+pi/2),e1.T).T - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # direction of line # start spiral DubinsAirplaneSolution['c_s'] = cls DubinsAirplaneSolution['psi_s'] = anglstart+pi/2 DubinsAirplaneSolution['lamda_s'] = -1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-end spiral DubinsAirplaneSolution['c_ei'] = ci - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T DubinsAirplaneSolution['psi_ei'] = theta+pi/2 DubinsAirplaneSolution['lamda_ei'] = -1 DubinsAirplaneSolution['k_ei'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cre - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = anglend-pi/2-psii DubinsAirplaneSolution['lamda_e'] = 1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from straight-line to intermediate spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_ei: switch from intermediate spiral to # end spiral DubinsAirplaneSolution['w_ei'] = zi - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['q_ei'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend),np.array([1,0,0]).T) elif idx == 4: # left-straight-right-left # path specific calculations ell = np.linalg.norm(ci[0:2] - cls[0:2],ord=2) theta = atan2( ci[1] - cls[1], ci[0] - cls[0]) theta2 = acos(2*R/ell) dist1 = R*fmod(2*pi-fmod(theta+theta2,2*pi) + fmod(anglstart+pi/2,2*pi),2*pi) dist2 = R*fmod(2*pi-fmod(theta+theta2-pi,2*pi)+fmod(chii-pi/2,2*pi),2*pi) dist3 = fabs(R_min*psii) w1 = cls + R*np.dot(rotz(theta+theta2),e1.T).T + np.array([0, 0, -dist1*tan(gam)]).T w2 = ci + R*np.dot(rotz(-pi+theta+theta2),e1.T).T - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T q1 = (w2-w1)/np.linalg.norm(w2-w1,ord=2) # start spiral DubinsAirplaneSolution['c_s'] = cls DubinsAirplaneSolution['psi_s'] = anglstart+pi/2 DubinsAirplaneSolution['lamda_s'] = -1 DubinsAirplaneSolution['k_s'] = 0 # intermediate-end spiral DubinsAirplaneSolution['c_ei'] = ci - np.array([0, 0, -(dist2+dist3)*tan(gam)]).T DubinsAirplaneSolution['psi_ei'] = fmod(theta+theta2-pi,2*pi) DubinsAirplaneSolution['lamda_ei'] = 1 DubinsAirplaneSolution['k_ei'] = 0 # end spiral DubinsAirplaneSolution['c_e'] = cle - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['psi_e'] = anglend+pi/2+psii DubinsAirplaneSolution['lamda_e'] = -1 DubinsAirplaneSolution['k_e'] = 0 # hyperplane H_s: switch from first to second spiral DubinsAirplaneSolution['w_s'] = w1 DubinsAirplaneSolution['q_s'] = q1 # hyperplane H_l: switch from straight-line to intermediate spiral DubinsAirplaneSolution['w_l'] = w2 DubinsAirplaneSolution['q_l'] = q1 # hyperplane H_ei: switch from intermediate spiral to # end spiral DubinsAirplaneSolution['w_ei'] = zi - np.array([0, 0, -dist3*tan(gam)]).T DubinsAirplaneSolution['q_ei'] = np.array([cos(chii), sin(chii), 0]).T # hyperplane H_e: end of Dubins path DubinsAirplaneSolution['w_e'] = ze DubinsAirplaneSolution['q_e'] = np.dot(rotz(anglend), np.array([1, 0, 0]).T) if DubinsAirplaneSolution['case'] == 4: print '### Not Implemented Case' return DubinsAirplaneSolution def drawline(w1=None, q1=None, w2=None, q2=None, step=None): # extract line path r = w1 # propagate line until cross half plane s = 0 NrNc = r.shape if len(NrNc) == 1: NrNc_ind = NrNc[0] last_col = r[:] else: NrNc_ind = NrNc[1] last_col = r[:,NrNc[1]-1] r.shape = (3,1) while np.dot( (last_col - w2).T,q2 ) <= 0: s = s + step w1.shape = (3,1) q1.shape = (3,1) new_col = w1+s*q1 new_col.shape = (3,1) r = np.hstack( (r, new_col) ) NrNc = r.shape if len(NrNc) == 1: NrNc_ind = NrNc[0] last_col = r[:] else: NrNc_ind = NrNc[1] last_col = r[:,NrNc[1]-1] return r def drawspiral(R=None, gam=None, c=None, psi=None, lam=None, k=None, w=None, q=None, step=None): # extract spiral path r = np.zeros((1,1)) r = c.T + R*np.array( [cos(psi), sin(psi), 0] ).T r = r.T # determine number of required crossings of half plane NrNc = r.shape if len(NrNc) ==1 : NrNc_ind = NrNc[0] halfplane = np.dot( (r[0:2]-w[0:2].T),q[0:2] ) else: NrNc_ind = NrNc[1] halfplane = np.dot( (r[0:2,NrNc_ind-1]-w[0:2].T),q[0:2] ) if (halfplane > 0).all() : required_crossing = 2 * ( k + 1 ) else: required_crossing = 2 * k + 1 # propagate spiral until cross half plane the right number of times s = 0 r.shape = (3,1) while ( required_crossing > 0 ) or ( (halfplane <= 0).all() ): s = s +step new_col = (c + R * np.array( [ cos(lam*s+psi), sin(lam*s+psi), -s*tan(gam)] ).T ) new_col.shape = (3,1) r = np.hstack( (r, new_col) ) NrNc = r.shape if len(NrNc)==1 : NrNc_ind = NrNc[0] if np.sign( halfplane ) != np.sign( np.dot((r[0:2]-w[0:2].T),q[0:2]) ): halfplane = np.dot( ( r[0:2] - w[0:2].T ), q[0:2] ) required_crossing = required_crossing - 1 else: NrNc_ind = NrNc[1] if np.sign(halfplane) != np.sign( np.dot( (r[0:2,NrNc_ind-1]-w[0:2].T ), q[0:2]) ): halfplane = np.dot( (r[0:2,NrNc_ind-1] - w[0:2] ).T, q[0:2] ) required_crossing = required_crossing - 1 return r def ExtractDubinsAirplanePath(DubinsAirplaneSolutions=None): # Extract the Dubins Airplane Solution in vector form step = 0.01 if DubinsAirplaneSolutions['case'] == 1: # spiral - line - spiral r1 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'], DubinsAirplaneSolutions['c_s'], DubinsAirplaneSolutions['psi_s'], DubinsAirplaneSolutions['lamda_s'], DubinsAirplaneSolutions['k_s'], DubinsAirplaneSolutions['w_s'], DubinsAirplaneSolutions['q_s'],step) r2 = drawline(DubinsAirplaneSolutions['w_s'], DubinsAirplaneSolutions['q_s'], DubinsAirplaneSolutions['w_l'], DubinsAirplaneSolutions['q_l'], step) r3 = drawspiral(DubinsAirplaneSolutions['R'], DubinsAirplaneSolutions['gamma'], DubinsAirplaneSolutions['c_e'], DubinsAirplaneSolutions['psi_e'], DubinsAirplaneSolutions['lamda_e'], DubinsAirplaneSolutions['k_e'], DubinsAirplaneSolutions['w_e'], DubinsAirplaneSolutions['q_e'], step) path = r1 r = np.hstack((r1,r2)) r = np.hstack((r,r3)) elif DubinsAirplaneSolutions['case'] == 2: # spiral - spiral - line -spiral r1 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'],DubinsAirplaneSolutions['c_s'],DubinsAirplaneSolutions['psi_s'],DubinsAirplaneSolutions['lamda_s'],DubinsAirplaneSolutions['k_s'],DubinsAirplaneSolutions['w_s'],DubinsAirplaneSolutions['q_s'],step) r2 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'],DubinsAirplaneSolutions['c_si'],DubinsAirplaneSolutions['psi_si'],DubinsAirplaneSolutions['lamda_si'],DubinsAirplaneSolutions['k_si'],DubinsAirplaneSolutions['w_si'],DubinsAirplaneSolutions['q_si'],step) r3 = drawline(DubinsAirplaneSolutions['w_si'],DubinsAirplaneSolutions['q_si'],DubinsAirplaneSolutions['w_l'],DubinsAirplaneSolutions['q_l'],step) r4 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'],DubinsAirplaneSolutions['c_e'],DubinsAirplaneSolutions['psi_e'],DubinsAirplaneSolutions['lamda_e'],DubinsAirplaneSolutions['k_e'],DubinsAirplaneSolutions['w_e'],DubinsAirplaneSolutions['q_e'],step) path = r1 r = np.hstack((r1,r2)) r = np.hstack((r,r3)) r = np.hstack((r,r4)) elif DubinsAirplaneSolutions['case'] == 3: # spiral - line - spiral - spiral r1 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'],DubinsAirplaneSolutions['c_s'],DubinsAirplaneSolutions['psi_s'],DubinsAirplaneSolutions['lamda_s'],DubinsAirplaneSolutions['k_s'],DubinsAirplaneSolutions['w_s'],DubinsAirplaneSolutions['q_s'],step) r2 = drawline(DubinsAirplaneSolutions['w_s'],DubinsAirplaneSolutions['q_s'],DubinsAirplaneSolutions['w_l'],DubinsAirplaneSolutions['q_l'],step) r3 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'],DubinsAirplaneSolutions['c_ei'],DubinsAirplaneSolutions['psi_ei'],DubinsAirplaneSolutions['lamda_ei'],DubinsAirplaneSolutions['k_ei'],DubinsAirplaneSolutions['w_ei'],DubinsAirplaneSolutions['q_ei'],step) r4 = drawspiral(DubinsAirplaneSolutions['R'],DubinsAirplaneSolutions['gamma'],DubinsAirplaneSolutions['c_e'],DubinsAirplaneSolutions['psi_e'],DubinsAirplaneSolutions['lamda_e'],DubinsAirplaneSolutions['k_e'],DubinsAirplaneSolutions['w_e'],DubinsAirplaneSolutions['q_e'],step) path = r1 r = np.hstack((r1,r2)) r = np.hstack((r,r3)) r = np.hstack((r,r4)) return r def PrintSolutionAgainstMATLAB(DubinsAirplaneSolution=None): print 'DubinsAirplaneSolution = ' print '\n' print 'case:\t\t ' + str(DubinsAirplaneSolution['case']) print 'p_s:\t\t' + str(DubinsAirplaneSolution['p_s']) + '\n' print 'angl_s:\t\t' + str(DubinsAirplaneSolution['angl_s']) + '\n' print 'p_e:\t\t' + str(DubinsAirplaneSolution['p_e']) + '\n' print 'R:\t\t' + str(DubinsAirplaneSolution['R']) print 'gamma:\t\t' + str(DubinsAirplaneSolution['gamma']) print 'L:\t\t' + str(DubinsAirplaneSolution['L']) print 'c_s:\t\t' + str(DubinsAirplaneSolution['c_s']) + '\n' print 'psi_s:\t\t' + str(DubinsAirplaneSolution['psi_s']) + '\n' print 'lamda_s:\t\t' + str(DubinsAirplaneSolution['lamda_s']) print 'lamda_si:\t\t' + str(DubinsAirplaneSolution['lamda_si']) print 'k_s:\t\t' + str(DubinsAirplaneSolution['k_s']) print 'c_ei:\t\t' + str(DubinsAirplaneSolution['c_ei'].T) + '\n' print 'c_si:\t\t' + str(DubinsAirplaneSolution['c_si'].T) + '\n' print 'psi_ei:\t\t' + str(DubinsAirplaneSolution['psi_ei']) print 'lamda_e:\t\t' + str(DubinsAirplaneSolution['lamda_e']) print 'k_e:\t\t' + str(DubinsAirplaneSolution['k_e']) print 'w_s:\t\t' + str(DubinsAirplaneSolution['w_s']) + '\n' print 'q_s:\t\t' + str(DubinsAirplaneSolution['q_s']) + '\n' print 'w_si:\t\t' + str(DubinsAirplaneSolution['w_si'].T) + '\n' print 'q_si:\t\t' + str(DubinsAirplaneSolution['q_si'].T) + '\n' print 'w_l:\t\t' + str(DubinsAirplaneSolution['w_l']) + '\n' print 'q_l:\t\t' + str(DubinsAirplaneSolution['q_l']) + '\n' print 'w_ei:\t\t' + str(DubinsAirplaneSolution['w_ei'].T) + '\n' print 'q_ei:\t\t' + str(DubinsAirplaneSolution['q_ei'].T) + '\n' print 'w_e:\t\t' + str(DubinsAirplaneSolution['w_e']) + '\n' print 'q_e:\t\t' + str(DubinsAirplaneSolution['q_e']) + '\n' print 'angl_e:\t\t' + str(DubinsAirplaneSolution['angl_e']) + '\n'
# __DUBINSAIRPLANEFUNCTIONS__ # A small set of helping functions # # Authors: # Kostas Alexis ([email protected]) import __builtin__ def max(a, b): # just a simple max function between 2 values if a >=b: return a else: return b def min(a, b=0, nargout=0): # just a simple min function between 2 values if a <= b: return a else: return b
# __DUBINSAIRPLANEFUNCTIONS__ # A small set of helping functions # # Authors: # Kostas Alexis ([email protected]) import __builtin__ def max(a, b): # just a simple max function between 2 values if a >=b: return a else: return b def min(a, b=0, nargout=0): # just a simple min function between 2 values if a <= b: return a else: return b