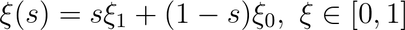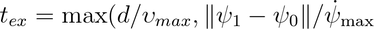Holonomic Vehicle Boundary Value Solver

Explicit solutions to the problem of point-to-point navigation of a holonomic vehicle operating within an obstacle-free world are straightforward. More specifically, a 6-degrees of freedom (DOF) vehicle that can be approximated to assume only small roll and pitch angles can be approximated using a very simple Boundary Value Solver (BVS). Considering an approximate state vector ξ = [x,y,z,ψ] (where x,y,z are the 3 position states and ψ the yaw angle), the path from the state configuration ξ0 to ξ1 is given by: 

And considering a limitation on the possible rate of change of the yaw angle \dψ/dt|max and the maximum linear velocity υmax, the execution time is:

with d used to denote the Euclidean distance. 

Python Implementation

File: HoverModeMain.py

#       __HOVERMODEMAIN__
#       This is the main file to execute examples of the Hover mode
#
#       Authors: 
#       Kostas Alexis (kalexis@unr.edu)

from HoverFunctions import * 
from PlottingTools import plot3
import numpy as np
import time
import sys

pi = np.pi
verbose_flag = 0
plot_flag = 1

point_0 = np.array([0,0,0,0])
point_1 = np.array([10,10,10,pi/4])

class ExecutionFlags(object):
    """
        Execution flags
    """  
    def __init__(self, verbose_flag, plot_flag):
        self.verbose = verbose_flag
        self.plot = plot_flag

class VehicleParameters(object):
    """
        Vehicle Parameters
    """ 
    def __init__(self, v_max, psi_rate_max):
        self.v_max = v_max
        self.psi_rate_max = psi_rate_max
    
def main():
    # Example main for the Hover mode
    t0 = time.clock()
    VehiclePars = VehicleParameters( 4, pi/4,) 
    ExFlags = ExecutionFlags( verbose_flag,plot_flag )
    
    flag_nc = 0
    fname = 'hover_solution.txt'
    HoverSolution = AssembleHoverSolution(point_0, point_1, VehiclePars.v_max, VehiclePars.psi_rate_max)
    path_hover = HoverSolution['connection']
    np.savetxt( fname, path_hover, delimiter = ',' ) 
    if ExFlags.plot :
            print '### Hover solution plot'
            plot3( path_hover[:,0], path_hover[:,1], path_hover[:,2], 'o', 'g' )
  

def testAllCases():
    main()
    print 'Press any button to continue'
    raw_input()
        

if __name__ == "__main__":
    testAllCases()

File: HoverFunctions.py

#       __HOVERFUNCTIONS__
#       This is the main file to execute functions of the Hover mode
#
#       Authors: 
#       Kostas Alexis (kalexis@unr.edu)


from __future__ import division
import numpy as np
from math import tan, sin, cos, atan2, fmod, acos, asin, pow, sqrt, fabs,atan
from ElementaryFunctions import max, min

pi = np.pi

HoverSolution = { }
HoverSolution['connection'] = np.zeros((2,4));
HoverSolution['distance'] = 0;
HoverSolution['t_ex'] = 0;

def computeHoverConnection(point_0=None, point_1=None):
    L = np.array([point_0, point_1])
    return L

def computeHoverConnectionDistance(point_0=None, point_1=None):
    dist_ = sqrt( pow(point_1[0]-point_0[0],2) + pow(point_1[1]-point_0[1],2) + pow(point_1[2]-point_0[2],2) ) 
    return dist_

def computeHoverConnectionTime(point_0=None,point_1=None,v_max=None,psi_rate_max=None):
    dist_ = computeHoverConnectionDistance(point_0, point_1)
    t_ex = max( dist_/v_max, fabs(point_1[3]-point_0[3])/psi_rate_max)
    return t_ex

def AssembleHoverSolution(point_0=None,point_1=None,v_max=None,psi_rate_max=None):
    L = computeHoverConnection(point_0, point_1)
    dist_ = computeHoverConnectionDistance(point_0, point_1)
    t_ex = computeHoverConnectionTime(point_0, point_1, v_max, psi_rate_max)
    HoverSolution['connection'] = L
    HoverSolution['distance'] = dist_
    HoverSolution['t_ex'] = t_ex
    return HoverSolution
    

File: PlottingTools.py

#       __PLOTTINGTOOLS__
#       Plotting functions
#
#       Authors: 
#       Kostas Alexis (kalexis@unr.edu)

import matplotlib.pyplot as mpplot
from matplotlib import pyplot
import pylab
from mpl_toolkits.mplot3d import Axes3D
    
def plot3(a,b,c,mark="o",col="r"):
    # mimic matlab plot3
    from matplotlib import pyplot
    import pylab
    pylab.ion()
    fig = pylab.figure()
    ax = Axes3D(fig)
    ax.invert_zaxis()
    ax.invert_xaxis()
    ax.set_aspect('equal', 'datalim')
    ax.plot(a, b,c,color=col,marker=mark)
    fig.show()