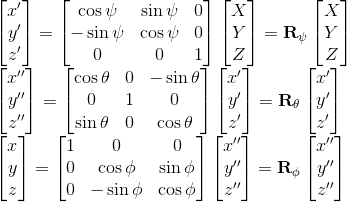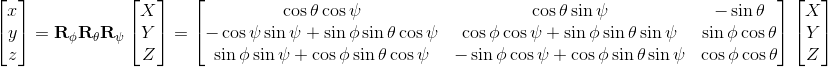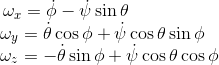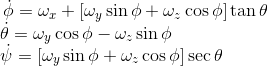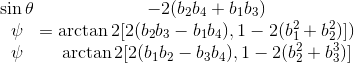Frame Rotations and Representations

Euler Angles

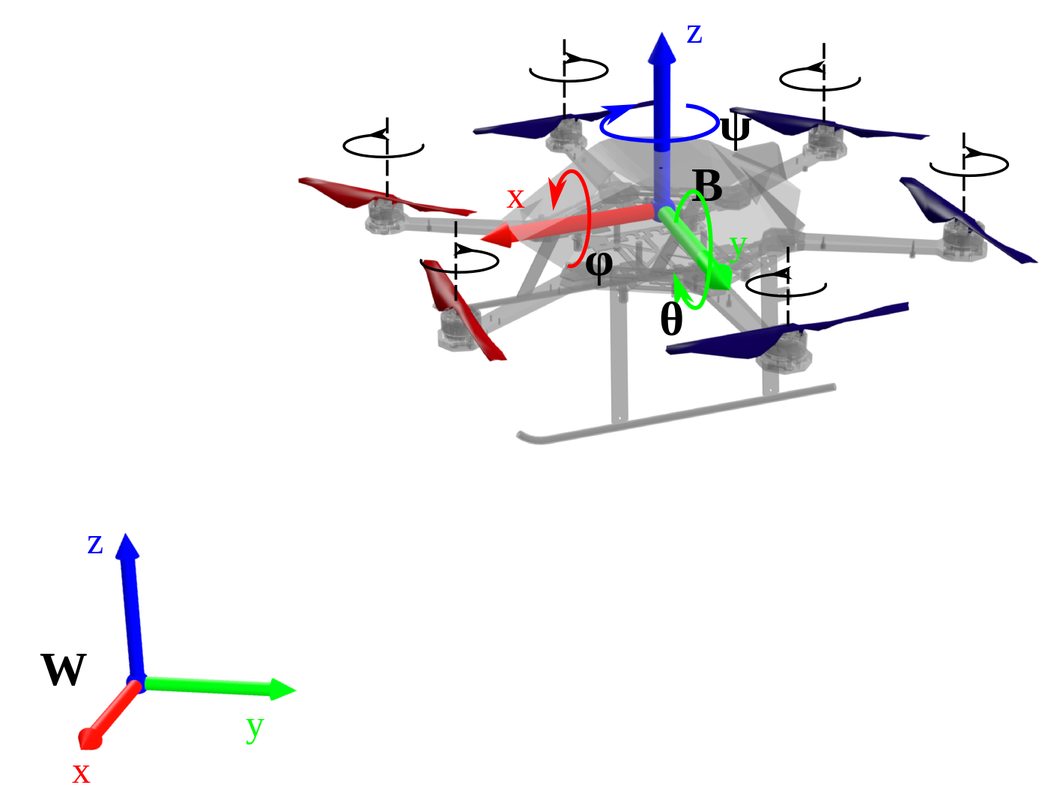
Euler angles are a method to determine and represent the rotation of a body as expressed in a given coordinate frame. They are defined as three (chained) rotations relative to the three major axes of the coordinate frame. Euler angles are typically representes as phi (φ) for x-axis rotation, theta (θ) for y-axis rotation, and psi (ψ) for z-axis rotation. Any orientation can be described through a combination of these angles. Figure 1 represents the Euler angles for a multirotor aerial robot. 

These elemental rotations can take place about the axes of the fixed coordinate frame (extrinsic rotations) or about the axes of a rotating coordinate frame (e.g. one attached on the vehicle), which is initially aligned with the fixed one, and modifies its orientation after each elemental rotation (intrinsic rotations). Without accounting the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups:

• Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)
  
• Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).

Figure 1: Euler angles represented for a multirotor aerial robot. 

As seen there are many ways to do this set of rotations - with the variations be based on the order of rotations. All would be formally acceptable, but some are much more commonly used than others. 

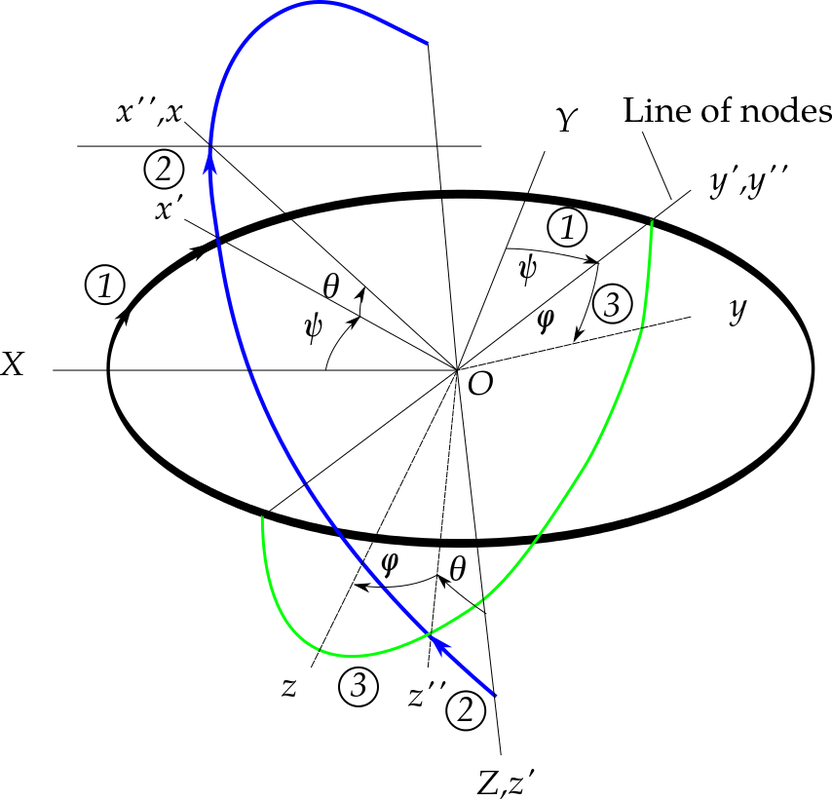
​Among them, one that is particuarly widely used is the following: start with the body fixed-frame (attached on the vehicle) (x,y,z) aligned with the inertial frame (X,Y,Z), and then perform 3 rotations to re-orient the body frame. 

1. Rotate by ψ about Z : x', y', z'
2. Rotate by θ about y' : x'', y'', z''
3. Rotate by φ about x'' " x, y, z

Euler angles: 

• ψ : Yaw (heading)
• θ : Pitch
• φ : Roll

To learn more about different conventions, please visit: 

• https://en.wikipedia.org/wiki/Euler_angles
• http://www.mathworks.com/discovery/euler-angles.html
• http://mathworld.wolfram.com/EulerAngles.html

​

Figure 2: Representation of the Euler Angles.

We can write the aforementioned set of rotations as: 

which combines to give:

To get the angular velocity, we will have to include three terms, namely the time derivative of ψ around Z, the time derivative of θ around y' and the time derivative of φ around x''. These three terms are combined to give the vector of angular velocities ω. The final result takes the form:

And in inverse form:

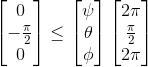
Note that one has to take care for singularities such as the pitch angle at plus/minus 90 degrees. A typical set of Euler Angles considers the following set of limitations:

Quaternions

Theorem by Euler states that any given sequence of rotations can be represented as a signle rotation about a single fixed axis. The concept of Quaternions provides a convenient parametrization of this effective axis and the rotation angle: 

Notes:

• $||\bar{b}|| =1$ abd thus there are only 3 degrees of freedom in this formulation, and
• if $\bar{b}$ represents the rotational transformation from the reference frame ($\alpha$) to the frame $b$, the frame $\alpha$ is aligned with frame $b$ if frame $\alpha$ is rotated by $\zeta$ about $\bar{E}$

This representation is connected with the Euler angles form, according to the following expression:

This representation has the great advantage of being: 

• Singularity-free and
• Computationally efficient to do state propagation (typically within an Extended Kalman Filter)

On the other hand, it has one main disadvantage, namely being far less intuitive. 

Euler to-and-from Quaternions Python Implementation 

File: QuatEulerMain.py

#       __QUATEULERMAIN__
#       This main file demonstrates functions for handling 
#       and manipulating quaternios and Euler Angles
#
#       Authors: 
#       Kostas Alexis (kalexis@unr.edu)

from numpy import *
import numpy as np
from QuatEulerFunctions import *

# demo values
q_ = np.array([0.25,0.5,0.1,0.2])

print 'Quaternion: '
print q_

rpy_ = quat2rpy(q_)
print 'Euler angles'
print rpy_

quat_ = rpy2quat(rpy_)
print 'Recovered quaternion:'
print quat_

rot_ = quat2r(quat_)
print 'Recovered rotation matrix:'
print rot_

rpy_rec_ = r2rpy(rot_)
print 'Recovered Euler'
print rpy_rec_

q_norm_ = normalized(q_)
print 'Normalized quaternion:'
print q_norm_

File: QuatEulerFunctions.py

#       __QUATEULERFUNCTIONS__
#       This file implements functions for handling 
#       and manipulating quaternios and Euler Angles
#
#       Authors: 
#       Kostas Alexis (kalexis@unr.edu)

from numpy import *
import numpy as np

def quat2r(q_AB=None):
    C_AB = np.zeros((3,3))
    C_AB[0,0] = q_AB[0]*q_AB[0] - q_AB[1]*q_AB[1] - q_AB[2]*q_AB[2] + q_AB[3]*q_AB[3]
    C_AB[0,1] = q_AB[0]*q_AB[1]*2.0 + q_AB[2]*q_AB[3]*2.0
    C_AB[0,2] = q_AB[0]*q_AB[2]*2.0 - q_AB[1]*q_AB[3]*2.0
    
    C_AB[1,0] = q_AB[0]*q_AB[1]*2.0 - q_AB[2]*q_AB[3]*2.0
    C_AB[1,1] = -q_AB[0]*q_AB[0] + q_AB[1]*q_AB[1] - q_AB[2]*q_AB[2] + q_AB[3]*q_AB[3]
    C_AB[1,2] = q_AB[0]*q_AB[3]*2.0 - q_AB[1]*q_AB[2]*2.0
    
    C_AB[2,0] = q_AB[0]*q_AB[2]*2.0 + q_AB[1]*q_AB[3]*2.0
    C_AB[2,1] = q_AB[0]*q_AB[3]*(-2.0) + q_AB[1]*q_AB[2]*2.0
    C_AB[2,2] = -q_AB[0]*q_AB[0] - q_AB[1]*q_AB[1] + q_AB[2]*q_AB[2] + q_AB[3]*q_AB[3]
    return C_AB

def quat2rpy(q_AB=None):
    C = quat2r(q_AB)
    theta = np.arcsin(-C[2,0])
    phi = np.arctan2(C[2,1],C[2,2])
    psi = np.arctan2(C[1,0],C[0,0])
    rpy = np.zeros((3,1))
    rpy[0] = phi
    rpy[1] = theta
    rpy[2] = psi
    return rpy

def rpy2quat(rpy=None):
    r = rpy[0] 
    p = rpy[1]
    y = rpy[2]
    cRh = np.cos(r/2)
    sRh = np.sin(r/2)
    cPh = np.cos(p/2)
    sPh = np.sin(p/2)
    cYh = np.cos(y/2)
    sYh = np.sin(y/2)
    qs_cmpl = np.array([ -(np.multiply(np.multiply(sRh,cPh),cYh) - np.multiply(np.multiply(cRh,sPh),sYh)),
                         -(np.multiply(np.multiply(cRh,sPh),cYh) + np.multiply(np.multiply(sRh,cPh),sYh)),
                         -(np.multiply(np.multiply(cRh,cPh),sYh) - np.multiply(np.multiply(sRh,sPh),cYh)),
                         np.multiply(np.multiply(cRh,cPh),cYh) + np.multiply(np.multiply(sRh,sPh),sYh)])
    qs = np.real(qs_cmpl)
    return qs

def r2rpy(C=None):
    theta = np.arcsin(-C[2,0])
    phi = np.arctan2(C[2,1],C[2,2])
    psi = np.arctan2(C[1,0],C[0,0])
    rpy = np.zeros((3,1))
    rpy[0] = phi
    rpy[1] = theta
    rpy[2] = psi
    return rpy

def normalized(x=None):
    y=x/np.sqrt(np.dot(x,x))
    return y

Euler to-and-from Quaternions MATLAB Implementation

File: QuatEulerMain.m

%        __QUATEULERMAIN__
%        This main file demonstrates functions for handling 
%        and manipulating quaternios and Euler Angles
% 
%        Authors: 
%        Shehryar Khattak (shehryar@nevada.unr.edu)

%Clear Workspace and Command Window
clear;clc;

%Demo Quaternion value
q = [0.25 0.5 0.1 0.2];

%Display Quaternion
fprintf('\n --- Quaternion --- \n')
disp(q');

%Normalize Quaternion
q_norm=q/norm(q);
fprintf('\n --- Normailized Quaternion --- \n');
disp(q_norm');

%Euler Angles
eul_ang=quat2rpy(q);
fprintf('\n --- Euler Angles --- \n')
fprintf('Roll=%f\nPitch=%f\nYaw=%f\n',eul_ang(1),eul_ang(2),eul_ang(3));

%Recovered Quaternion
q_rec=rpy2quat(eul_ang);
fprintf('\n --- Recovered Quaternion --- \n')
disp(q_rec');

%Rotation Matrix from Quaternion
rot_m=quat2r(q_rec);
fprintf('\n --- Rotation Matrix from Quaternion --- \n')
disp(rot_m);

%Recoverd Euler from Rotation Matrix
rpy_rec=r2rpy(rot_m);
fprintf('\n --- Recovered Euler Angles from Rotation Matrix --- \n');
fprintf('Roll=%f\nPitch=%f\nYaw=%f\n',rpy_rec(1),rpy_rec(2),rpy_rec(3));

File: quat2r.m

%        __Quaternion to Rotation Matrix__   
% 
%        Authors: 
%        Shehryar Khattak (shehryar@nevada.unr.edu)
%        Reference: http://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToMatrix/

%Convert Quaternion to Rotation Matrix
function [r] = quat2r(q)

    %Check if vector and if have it has enough input values
    if ~isvector(q) || (length(q))~=4 
        error('Input to quat2r must be a vector and must have 4 values')
    end
    
    %Initialize
    r=zeros(3,3);
    
    %Normailize Quaternion before using
    q=q/norm(q);
    
    %Quaternion components
    qw=q(1);
    qx=q(2);
    qy=q(3);
    qz=q(4);
    
    %Rotation Matrix Elements
    r(1,1) = 1 - 2*qy^2 - 2*qz^2;
    r(1,2) = 2*qx*qy - 2*qz*qw;
    r(1,3) = 2*qx*qz + 2*qy*qw;
    
    r(2,1) = 2*qx*qy + 2*qz*qw;
    r(2,2) = 1 - 2*qx^2 - 2*qz^2;
    r(2,3) = 2*qy*qz - 2*qx*qw;
    
    r(3,1) = 2*qx*qz - 2*qy*qw;
    r(3,2) = 2*qy*qz + 2*qx*qw;
    r(3,3) = 1 - 2*qx^2 - 2*qy^2;
    
    %Equivalent built-in MATLAB function: quat2rotm
end

File: quat2rpy.m

%        __Quaternion to Euler Angles__
% 
%        Authors: 
%        Shehryar Khattak (shehryar@nevada.unr.edu)
%        Reference: Beard, Randal W., and Timothy W. McLain. Small unmanned aircraft: Theory and practice. Princeton University Press, 2012. Appendix B, Page 259

%Convert Quaternion to Euler 
function [eul_ang] = quat2rpy(q)

    %Check if vector and if have it has enough input values
    if ~isvector(q) || (length(q))~=4 
        error('Input to quat2rpy must be a vector and must have 4 values')
    end
    
    %Normailize Quaternion before using
    q=q/norm(q);
    
    %Roll
    eul_ang(1)      =   atan2(   (2*(q(1)*q(2)+(q(3)*q(4)))) , (q(1)^2+q(4)^2-q(2)^2-q(3)^2) );
    %Pitch 
    eul_ang(2)      =   asin(    2*((q(1)*q(3))-(q(2)*q(4))) );
    %Yaw
    eul_ang(3)      =   atan2(   (2*(q(1)*q(4)+(q(2)*q(3)))) , (q(1)^2+q(2)^2-q(3)^2-q(4)^2) );    
    
    %Equivalent built-in MATLAB function: quat2eul
end

File: r2rpy.m

%        __Rotation Matrix to Euler Angles__   
% 
%        Authors: 
%        Shehryar Khattak (shehryar@nevada.unr.edu)       
%        Reference: http://nghiaho.com/?page_id=846


%Convert Rotation Matrix to Euler Angles
function [eul_ang]=r2rpy(rot_m)

    %Check if matrix and if have it has enough input values
    if ~ismatrix(rot_m) || numel(rot_m)~=9 
        error('Input to r2rpy must be a 3x3 matrix')
    end
    
    eul_ang(1)=atan2(rot_m(3,2),rot_m(3,3));    %ro - roll
    eul_ang(2)=atan2(-rot_m(3,1),sqrt(rot_m(3,2)^2+rot_m(3,3)^2)); %theta - pitch
    eul_ang(3)=atan2(rot_m(2,1),rot_m(1,1));    %psi - yaw
    
    %Equivalent built-in MATLAB function: eul2rotm    
end

File: rpy2quat.m

%        __Euler Angles to Quaternion__        
% 
%        Authors: 
%        Shehryar Khattak (shehryar@nevada.unr.edu)
%        Reference: Beard, Randal W., and Timothy W. McLain. Small unmanned aircraft: Theory and practice. Princeton University Press, 2012. Appendix B, Page 259

%Convert Euler anngles to Quaternion
function [q]=rpy2quat(eul_ang)
     
    %Check if vector and if have it has enough input values
    if ~isvector(eul_ang) || (length(eul_ang))~=3
        error('Input to eul_ang must be a vector and must have 3 values')
    end
    
    r=eul_ang(1)/2;
    p=eul_ang(2)/2;
    y=eul_ang(3)/2;
    
    q(1)= (cos(y)*cos(p)*cos(r)) + (sin(y)*sin(p)*sin(r)) ;
    q(2)= (cos(y)*cos(p)*sin(r)) - (sin(y)*sin(p)*cos(r)) ;
    q(3)= (cos(y)*sin(p)*cos(r)) + (sin(y)*cos(p)*sin(r)) ;
    q(4)= (sin(y)*cos(p)*cos(r)) - (cos(y)*sin(p)*sin(r)) ;
    
    %Equivalent built-in MATLAB function: eul2quat
end