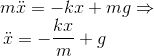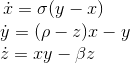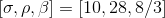Vehicle Dynamics Simulation using SimPy
A Quick Introduction to SimPy for ODE Simulations
|
Below, the basic concepts of SimPy - and how they apply to the problem of simulating Ordinary Differential Equations -will be overviewed.
1. Installation Execute the following steps:
You can now optionally the basic verification steps that SimPy's offers:
|
2. Characterizing a system using Ordinary Differential Equations
|
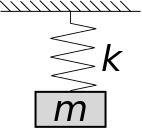
A dynamic system, say a mass-spring system, can be characterized by the relation between its state variables and its inputs. This relation is expressed in the form of differential equations (and in that case "Ordinary Differential Equations"). To derive the ODE representation, we rely on laws of physics with the level of accuracy and fidelity we consider appropriate for the specific task at hand.
The specifc system (shown in Figure 1) can be captured by the following secord order Ordinary Differential Equation (ODE): |
Figure 1: Sprin-mass system.
|
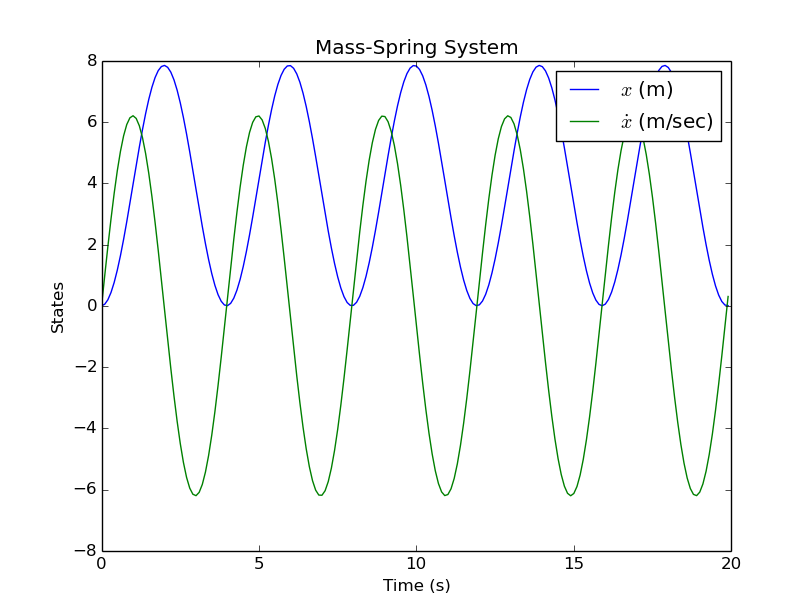
Simulating such a system with the help of SimPy is particularly simple as shown in the code section below.
from scipy.integrate import odeint from numpy import * import matplotlib.pyplot as plt def MassSpring(state,t): x = state[0] # position xd = state[1] # velocity # variables k = -5 # Nm m = 2 # kg g = 9.81 # m/s^2 # mass acceleration xdd = ((k*x)/m) + g return [xd, xdd] state0 = [0.0, 0.0] t = arange(0.0, 20.0, 0.1) state = odeint(MassSpring, state0, t) plt.plot(t, state) plt.xlabel('Time (s)') plt.ylabel('States') plt.title('Mass-Spring System') plt.legend(('$x$ (m)', '$\dot{x}$ (m/sec)')) plt.show() raw_input() |
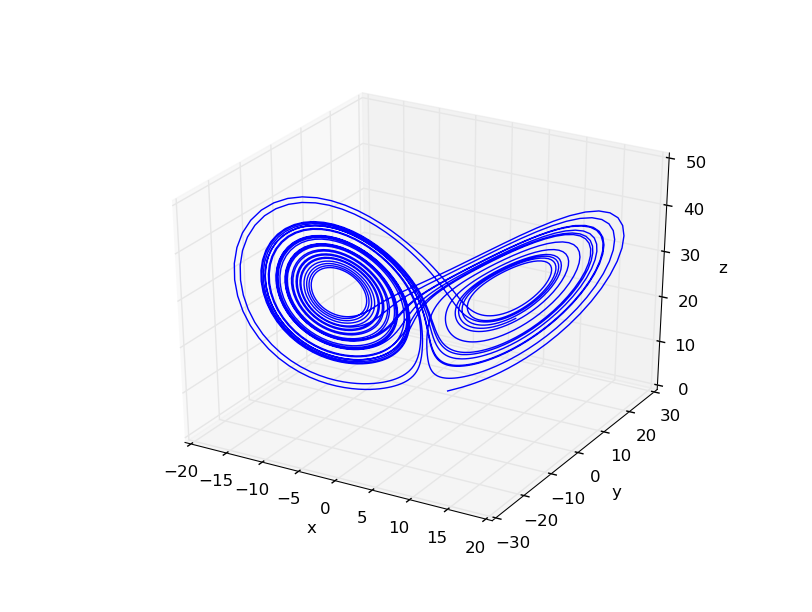
The aforementioned system is particularly simple as it is expressed using linear ODEs. A slightly more difficult case arises, when one has to deal with nonlinear systems. Take for example the case of the Lorenz Attractor, a well known nonlinear system actively used to illustrate concepts of the chaos theory. Its state equations are:
The parameters σ,ρ,β are dominating the response of the system and if ones sets them as:
Then the system exhibits chaotic behavior as shown in the simulation case study below.
from scipy.integrate import odeint from numpy import * import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D def Lorenz(state,t): x = state[0] y = state[1] z = state[2] # set the constants sigma = 10.0 rho = 28.0 beta = 8.0/3.0 xd = sigma * (y-x) yd = (rho-z)*x - y zd = x*y - beta*z return [xd, yd, zd] state0 = [2.0, 3.0, 4.0] t = arange(0.0, 30.0, 0.01) state = odeint(Lorenz, state0, t) fig = plt.figure() ax = fig.gca(projection='3D') ax.plot(state[:,0],state[:,1],state[:,2]) ax.set_xlabel('x') ax.set_ylabel('y') ax.set_zlabel('z') fig.show() raw_input() |
Figure 3: Lorenz Attractor expression chaotic behavior.
|
Simulation of a Quadrotor Aerial Robot
|
The classes/methods below implement the simulation of the vehicle dynamics of a quadrotor aerial robot. The system is considered to be captured using rigid body modeling and the four thrust vectors attached to it, while its self-response is only characterized by its mass and the cross-inertia terms. Within that framework, scipy is employed for the forward integration purposes of the state update, while direct calculations and linear algebra are employed for the moment/forces calculations as well as the coordinate system transformations.
|
File: main.py
from quadrotor_sims_params import * if __name__ == "__main__": fly_quadrotor()
File: quadrotor_sims_params.py
# __QUADROTORSIMSPARAMS__ # This file implements the sim parameters # simple quadrotor simulation tool # # Largely based on the work of https://github.com/nikhilkalige from quadrotor_dynamics import QuadrotorDynamics import numpy as np import random import time import matplotlib.pyplot as plt TURNS = 3 class SimulationParams(object): def __init__(self): self.mass = 1 self.Ixx = 0.0053 self.length = 0.2 self.Bup = 21.58 self.Bdown = 3.92 self.Cpmax = np.pi * 1800/180 self.Cn = TURNS self.gravity = 9.81 def get_acceleration(self, p0, p3): ap = { 'acc': (-self.mass * self.length * (self.Bup - p0) / (4 * self.Ixx)), 'start': (self.mass * self.length * (self.Bup - self.Bdown) / (4 * self.Ixx)), 'coast': 0, 'stop': (-self.mass * self.length * (self.Bup - self.Bdown) / (4 * self.Ixx)), 'recover': (self.mass * self.length * (self.Bup - p3) / (4 * self.Ixx)), } return ap def get_initial_parameters(self): p0 = p3 = 0.9 * self.Bup p1 = p4 = 0.1 acc_start = self.get_acceleration(p0, p3)['start'] p2 = (2 * np.pi * self.Cn / self.Cpmax) - (self.Cpmax / acc_start) return [p0, p1, p2, p3, p4] def get_sections(self, parameters): sections = np.zeros(5, dtype='object') [p0, p1, p2, p3, p4] = parameters ap = self.get_acceleration(p0, p3) T2 = (self.Cpmax - p1 * ap['acc']) / ap['start'] T4 = -(self.Cpmax + p4 * ap['recover']) / ap['stop'] aq = 0 ar = 0 sections[0] = (self.mass * p0, [ap['acc'], aq, ar], p1) temp = self.mass * self.Bup - 2 * abs(ap['start']) * self.Ixx / self.length sections[1] = (temp, [ap['start'], aq, ar], T2) sections[2] = (self.mass * self.Bdown, [ap['coast'], aq, ar], p2) temp = self.mass * self.Bup - 2 * abs(ap['stop']) * self.Ixx / self.length sections[3] = (temp, [ap['stop'], aq, ar], T4) sections[4] = (self.mass * p3, [ap['recover'], aq, ar], p4) return sections def fly_quadrotor(params=None): gen = SimulationParams() quadrotor = QuadrotorDynamics() if not params: params = gen.get_initial_parameters() sections = gen.get_sections(params) state = quadrotor.update_state(sections) plt.plot(state) plt.show() raw_input()
File: quadrotor_dynamics.py
# __QUADROTORDYNAMICS__ # This file implements the dynamics of a # simple quadrotor micro aerial vehicle # # Largely based on the work of https://github.com/nikhilkalige import numpy as np from scipy.integrate import odeint class QuadrotorDynamics(object): def __init__(self, save_state=True, config={}): """ Quadrotor Dynamics Parameters ---------- save_state: Boolean Decides whether the state of the system should be saved and returned at the end """ self.config = { # Define constants 'gravity': 9.81, # Earth gravity [m s^-2] # Define Vehicle Parameters 'mass': 1, # Mass [kg] 'length': 0.2, # Arm length [m] # Cross-Intertia [Ixx, Iyy, Izz] 'inertia': np.array([0.0053, 0.0053, 0.0086]), # [kg m^2] 'thrustToDrag': 0.018 # thrust to drag constant [m] } self.save_state = save_state self._dt = 0.005 # Simulation Step self.config.update(config) self.initialize_state() def initialize_state(self): self.state = { # Position [x, y, z] of the quadrotor in inertial frame 'position': np.zeros(3), # Velocity [dx/dt, dy/dt, dz/dt] of the quadrotor in inertial frame 'velocity': np.zeros(3), # Euler angles [phi, theta, psi] 'orientation': np.zeros(3), # Angular velocity [p, q, r] 'ang_velocity': np.zeros(3) } def motor_thrust(self, moments, total_thrust): """Compute Motor Thrusts Parameters ---------- moments : numpy.array [Mp, Mq, Mr] moments total_thrust : float The total thrust generated by all motors Returns ------- numpy.array The thrust generated by each motor [T1, T2, T3, T4] """ [Mp, Mq, Mr] = moments thrust = np.zeros(4) tmp1add = total_thrust + Mr / self.config['thrustToDrag'] tmp1sub = total_thrust - Mr / self.config['thrustToDrag'] tmp2p = 2 * Mp / self.config['length'] tmp2q = 2 * Mq / self.config['length'] thrust[0] = tmp1add - tmp2q thrust[1] = tmp1sub + tmp2p thrust[2] = tmp1add + tmp2q thrust[3] = tmp1sub - tmp2p return thrust / 4.0 def dt_eulerangles_to_angular_velocity(self, dtEuler, EulerAngles): """Euler angles derivatives TO angular velocities dtEuler = np.array([dphi/dt, dtheta/dt, dpsi/dt]) """ return np.dot(self.angular_rotation_matrix(EulerAngles), dtEuler) def acceleration(self, thrusts, EulerAngles): """Compute the acceleration in inertial reference frame thrust = np.array([Motor1, .... Motor4]) """ force_z_body = np.sum(thrusts) / self.config['mass'] rotation_matrix = self.rotation_matrix(EulerAngles) # print rotation_matrix force_body = np.array([0, 0, force_z_body]) return np.dot(rotation_matrix, force_body) - np.array([0, 0, self.config['gravity']]) def angular_acceleration(self, omega, thrust): """Compute the angular acceleration in body frame omega = angular velocity :- np.array([p, q, r]) """ [t1, t2, t3, t4] = thrust thrust_matrix = np.array([self.config['length'] * (t2 - t4), self.config['length'] * (t3 - t1), self.config['thrustToDrag'] * (t1 - t2 + t3 - t4)]) inverse_inertia = np.linalg.inv(self.inertia_matrix) p1 = np.dot(inverse_inertia, thrust_matrix) p2 = np.dot(inverse_inertia, omega) p3 = np.dot(self.inertia_matrix, omega) cross = np.cross(p2, p3) return p1 - cross def angular_velocity_to_dt_eulerangles(self, omega, EulerAngles): """Angular Velocity TO Euler Angles omega = angular velocity :- np.array([p, q, r]) """ rotation_matrix = np.linalg.inv(self.angular_rotation_matrix(EulerAngles)) return np.dot(rotation_matrix, omega) def moments(self, ref_acc, angular_vel): """Compute the moments Parameters ---------- ref_acc : numpy.array The desired angular acceleration that the system should achieve. This should be of form [dp/dt, dq/dt, dr/dt] angular_vel : numpy.array The current angular velocity of the system. This should be of form [p, q, r] Returns ------- numpy.array The desired moments of the system """ inverse_inertia = np.linalg.inv(self.inertia_matrix) p1 = np.dot(inverse_inertia, angular_vel) p2 = np.dot(self.inertia_matrix, angular_vel) cross = np.cross(p1, p2) value = ref_acc + cross return np.dot(self.inertia_matrix, value) def angular_rotation_matrix(self, EulerAngles): """Rotation matix for Angular Velocity <-> Euler Angles Conversion Use inverse of the matrix to convert from angular velocity to euler rates """ [phi, theta, psi] = EulerAngles cphi = np.cos(phi) sphi = np.sin(phi) cthe = np.cos(theta) sthe = np.sin(theta) cpsi = np.cos(psi) spsi = np.sin(psi) RotMatAngV = np.array([ [1, 0, -sthe], [0, cphi, cthe * sphi], [0, -spsi, cthe * cphi] ]) return RotMatAngV def rotation_matrix(self, EulerAngles): [phi, theta, psi] = EulerAngles cphi = np.cos(phi) sphi = np.sin(phi) cthe = np.cos(theta) sthe = np.sin(theta) cpsi = np.cos(psi) spsi = np.sin(psi) RotMat = np.array([[cthe * cpsi, sphi * sthe * cpsi - cphi * spsi, cphi * sthe * cpsi + sphi * spsi], [cthe * spsi, sphi * sthe * spsi + cphi * cpsi, cphi * sthe * spsi - sphi * cpsi], [-sthe, cthe * sphi, cthe * cphi]]) return RotMat @property def inertia_matrix(self): return np.diag(self.config['inertia']) def update_state(self, piecewise_args): """Run the state update equations for self._dt seconds Update the current state of the system. It runs the model and updates its state to self._dt seconds. Parameters ---------- piecewise_args : array It contains the parameters that are needed to run each section of the flight. It is an array of tuples. [(ct1, da1, t1), (ct2, da2, t2), ..., (ctn, dan, tn)] ct : float The collective thrust generated by all motors da : numpy.array The desired angular acceleration that the system should achieve. This should be of form [dp/dt, dq/dt, dr/dt] t: float Time for which this section should run and should be atleast twice self._dt """ if self.save_state: overall_time = 0 for section in piecewise_args: overall_time += section[2] overall_length = len(np.arange(0, overall_time, self._dt)) - (len(piecewise_args) - 1) # Allocate space for storing state of all sections final_state = np.zeros([overall_length + 100, 12]) else: final_state = [] # Create variable to maintain state between integration steps self._euler_dot = np.zeros(3) index = 0 for section in piecewise_args: (total_thrust, desired_angular_acc, t) = section if t < (2 * self._dt): continue ts = np.arange(0, t, self._dt) state = np.concatenate((self.state['position'], self.state['velocity'], self.state['orientation'], self.state['ang_velocity'])) output = odeint(self._integrator, state, ts, args=(total_thrust, desired_angular_acc)) output_length = len(output) # State update [self.state['position'], self.state['velocity'], self.state['orientation'], self.state['ang_velocity']] = np.split(output[output_length - 1], 4) if self.save_state: # Final state update final_state[index:(index + output_length)] = output index = index + output_length - 1 return final_state def _integrator(self, state, t, total_thrust, desired_angular_acc): """Callback function for scipy.integrate.odeint. At this point scipy is used to execute the forward integration Parameters ---------- state : numpy.array System State: [x, y, z, xdot, ydot, zdot, phi, theta, psi, p, q, r] t : float Time Returns ------- numpy.array Rates of the input state: [xdot, ydot, zdot, xddot, yddot, zddot, phidot, thetadot, psidot, pdot, qdot, rdot] """ # Position inertial frame [x, y, z] pos = state[:3] # Velocity inertial frame [x, y, z] velocity = state[3:6] euler = state[6:9] # Angular velocity omega = [p, q, r] omega = state[9:12] # Derivative of euler angles [dphi/dt, dtheta/dt, dpsi/dt] euler_dot = self._euler_dot # omega = self.dt_eulerangles_to_angular_velocity(euler_dot, euler) moments = self.moments(desired_angular_acc, omega) thrusts = self.motor_thrust(moments, total_thrust) # Acceleration in inertial frame acc = self.acceleration(thrusts, euler) omega_dot = self.angular_acceleration(omega, thrusts) euler_dot = self.angular_velocity_to_dt_eulerangles(omega, euler) self._euler_dot = euler_dot # [velocity : acc : euler_dot : omega_dot] # print 'Vel', velocity # print 'Acc', acc # print 'Euler dot', euler_dot # print 'omdega dot', omega_dot return np.concatenate((velocity, acc, euler_dot, omega_dot))