Motion Primitives-based Navigation Planning using Deep Collision Prediction
This paper contributes a method to design a novel navigation planner exploiting a learning-based collision prediction network. The neural network is tasked to predict the collision cost of each action sequence in a predefined motion primitives library in the robot's velocity-steering angle space, given only the current depth image and the estimated linear and angular velocities of the robot. Furthermore, we account for the uncertainty of the robot's partial state by utilizing the Unscented Transform and the uncertainty of the neural network model by using Monte Carlo dropout. The uncertainty-aware collision cost is then combined with the goal direction given by a global planner in order to determine the best action sequence to execute in a receding horizon manner. To demonstrate the method, we develop a resilient small flying robot integrating lightweight sensing and computing resources. A set of simulation and experimental studies, including a field deployment, in both cluttered and perceptually-challenging environments is conducted to evaluate the quality of the prediction network and the performance of the proposed planner.
Publication
Under Review
Video Results
Code
Coming soon.
Dataset
Coming soon.
Further Evaluation (additional to what is presented in the paper)
To evaluate ORACLE’s ability to negotiate novel environments in combination with highly degraded state estimates, we conducted simulation studies in two environments, namely a) environment 1 (Figure 1) that contains obstacles seen during the training phase, b) environment 2 (Figure 2) contains unseen obstacles and compare ORACLE with three more versions:
Environment 1: Environment with known obstacles: image link
- "naive" which utilizes the Collision Prediction Network (CPN) directly to calculate the collision cost without considering the uncertainty of the robot's partial state or that of the neural network.
- UT which utilizes the CPN and Unscented Transform to calculate the collision cost.
- MC which utilizes the CPN and Monte Carlo dropout to calculate the collision cost.
Environment 1: Environment with known obstacles: image link
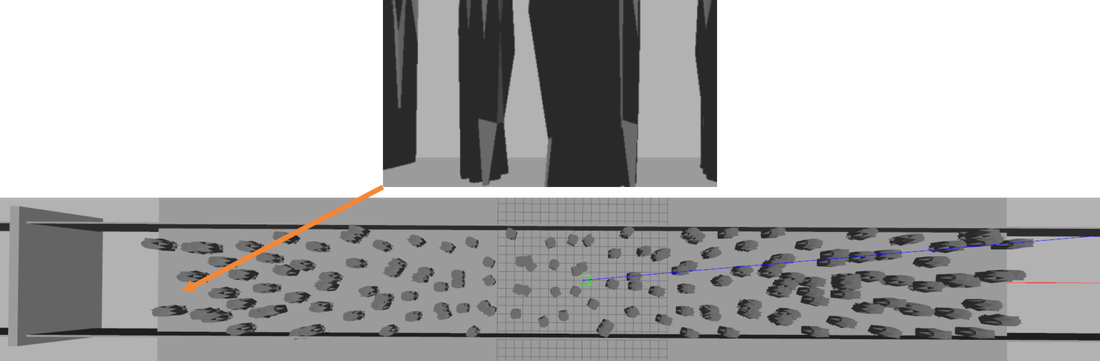
Fig. 1. Simulation environment 1 containing obstacles seen during the training phase and a depth image at specific location in the environment
The reference forward velocity in this simulation is 1.25 m/s.
* With perfect state estimation
The reference forward velocity in this simulation is 1.25 m/s.
* With perfect state estimation
| Planner | Collisions | Avg flight time before collision [sec] |
|---|---|---|
| Naive | 0/20 | 100 |
| UT | 0/20 | 100 |
| ORACLE | 0/20 | 100 |
* With deteriorated state estimation $s_t^{det}=[v_t^{det},\omega_t^{det}$, specifically $v_t^{det} = v_t - 1.0$m/s, $\omega_t^{det} = \omega_t + 0.1$rad/s
| Planner | Collisions | Avg flight time before collision [sec] |
|---|---|---|
| Naive | 14/20 | 63.5 |
| UT | 8/20 | 81.7 |
| ORACLE | 8/20 | 81.9 |
Environment 2: Environment with novel obstacles
Fig. 2. Simulation environment 2 containing novel obstacles unseen during the training phase and depth images at specific locations in the environment
The reference forward velocity in this simulation is 0.75 m/s.
* With perfect state estimation
The reference forward velocity in this simulation is 0.75 m/s.
* With perfect state estimation
| Planner | Collisions | Avg flight time before collision [sec] |
|---|---|---|
| Naive | 8/20 | 68 |
| UT | 5/20 | 89.5 |
| ORACLE | 5/20 | 89.1 |
* With deteriorated state estimation $s_t^{det}=[v_t^{det},\omega_t^{det}$, specifically $v_t^{det} = v_t - 0.5$m/s, $\omega_t^{det} = \omega_t + 0.1$rad/s
| Planner | Collisions | Avg flight time before collision [sec] |
|---|---|---|
| Naive | 11/20 | 61 |
| MC | 9/20 | 72 |
| ORACLE | 8/20 | 78.1 |
Two indicative simulations, one from each of the abovementioned environments are shown below.
|
|
|